توضیحات
حل عددی و تحلیلی معادله دیفرانسیل معمولی مرتبه دوم(ODE) ارتعاش آزاد سیستم جرم-فنر-دمپر با روش های اویلر پیشرو(Forward Euler) و رانگ-کوتا مرتبه چهار(Runge-Kutta) در نرم افزار متلب(MATLAB)
شرح پروژه:
در این پروژه حل عددی و تحلیلی معادله دیفرانسیل معمولی مرتبه دوم(ODE) ارتعاش آزاد سیستم جرم-فنر-دمپر با روش های اویلر پیشرو(Forward Euler) و رانگ-کوتا مرتبه چهار(Runge-Kutta) در نرم افزار متلب(MATLAB) کدنویسی شده است. در این پروژه علاوه بر کدهای متلب گزارش کامل فارسی پروژه را نیز دریافت خواهید کرد.
معادله دیفرانسیلی مرتبه دوم سیستم جرم-فنر-دمپر که دارای جرم m، ثابت فنریت k و ضریب میرایی y(t)، c جابجایی فنر (از نقطه تعادل خود) و f(t) نیروی خارجی یا ورودی سیستم است، به صورت زیر بیان می شود:
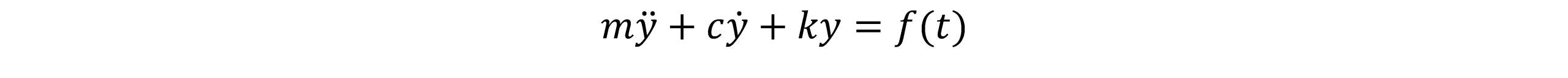
(1)
بازنویسی معادله دیفرانسیلی(1) به صورت زیر ارائه می شود:
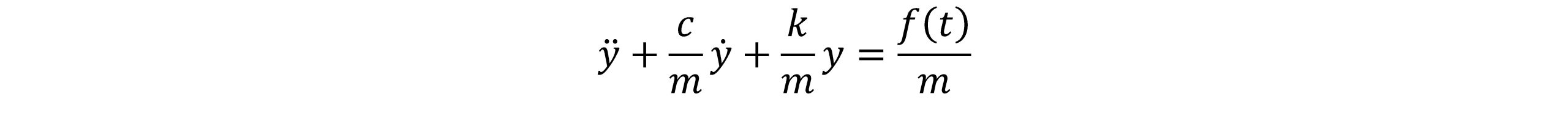
(2)
در حالت ارتعاش آزاد یا زمانیکه نیروی خارجی صفر باشد، معادله دیفرانسیلی(1) و (2) به صورت معادله دیفرانسیلی مرتبه دوم همگن بیان می شود:
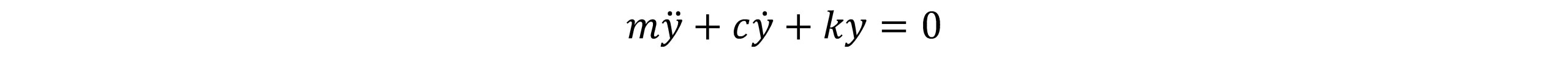
و یا می توان بصورت زیر بیان نمود:
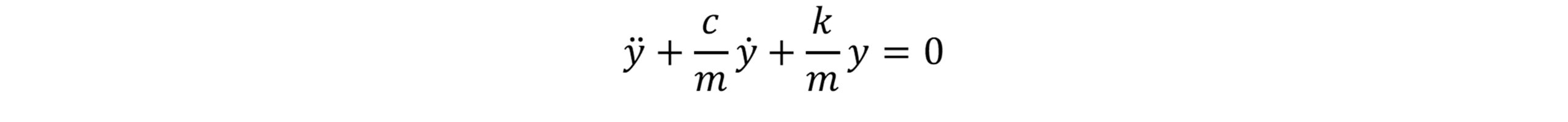
(3)
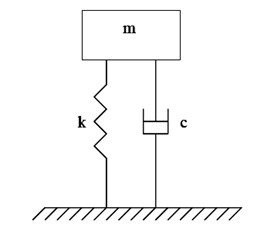
شکل سیستم جرم-فنر-دمپر.
جواب تحلیلی معادله دیفرانسیل معمولی مرتبه دوم سیستم جرم-فنر-دمپر:
جواب تحلیلی معادله دیفرانسیلی مرتبه اول باتوجه به شرایط اولیه y(0)=10 و y'(0)=5 به صورت معادله زیر بدست آمده است.
نمودار جواب های تحلیلی سیستم جرم-فنر-دمپر:
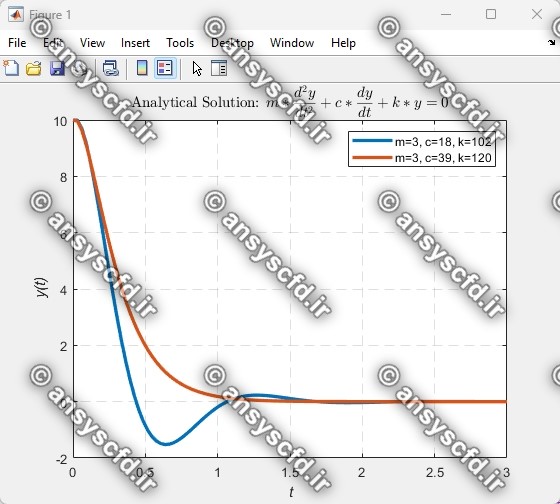
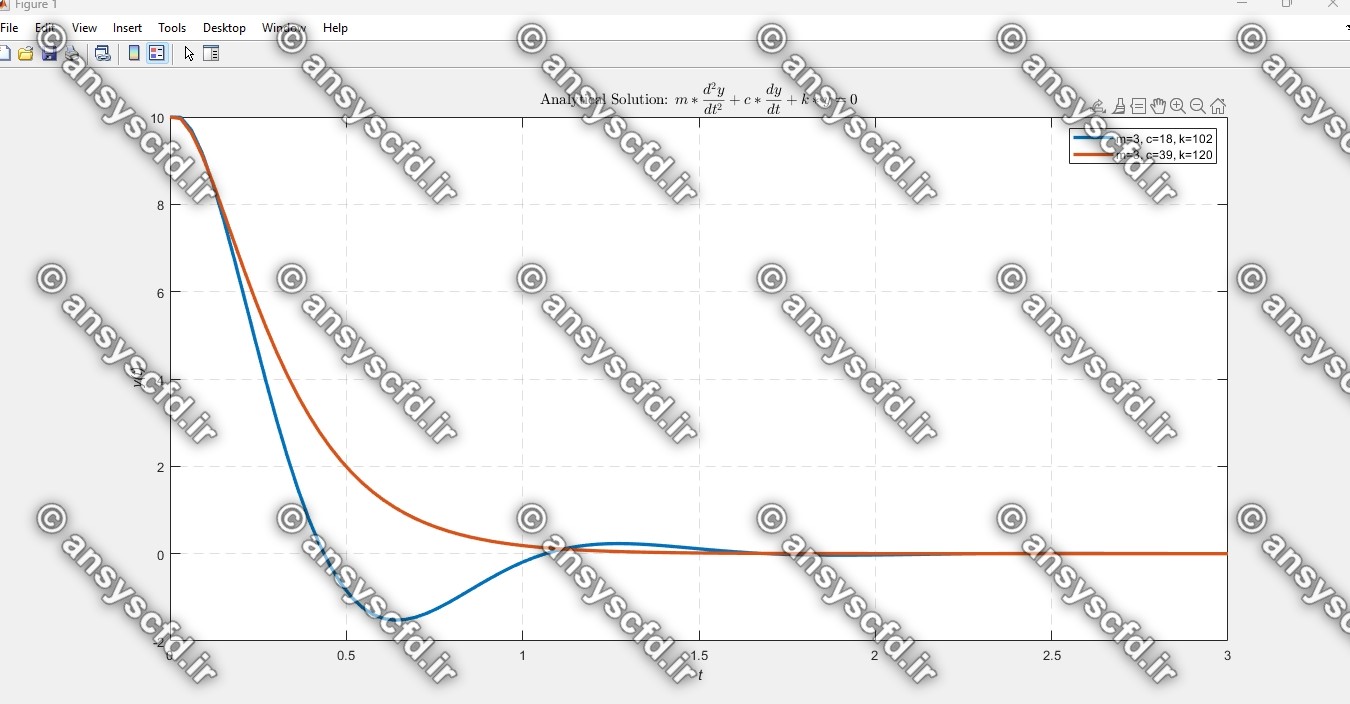
کدنویسی متلب روش های عددی اویلر پیشرو(Forward Euler)، و رانگ-کوتا مرتبه چهار (Runge-Kutta)
کدنویسی در متلب برای روش های عددی اویلر پیشرو(Forward Euler)، و رانگ-کوتا مرتبه چهار(Runge-Kutta) انجام شده است.
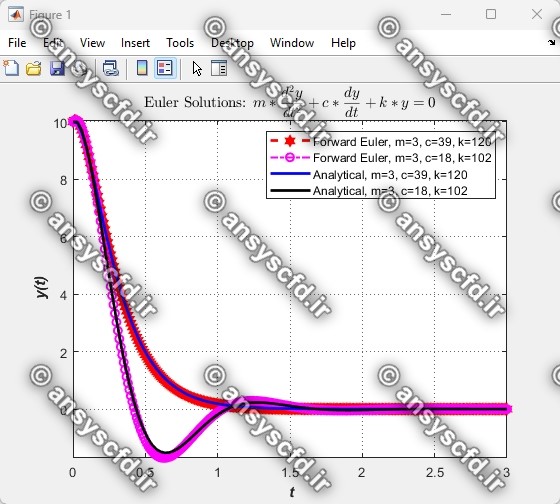
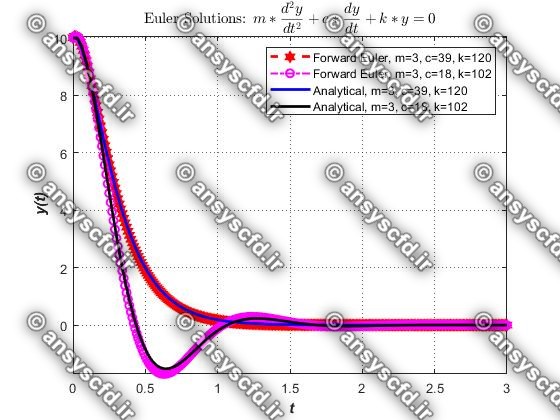
نتایج مقایسه روش های اویلر و رانگ-کوتا و جواب تحلیلی:
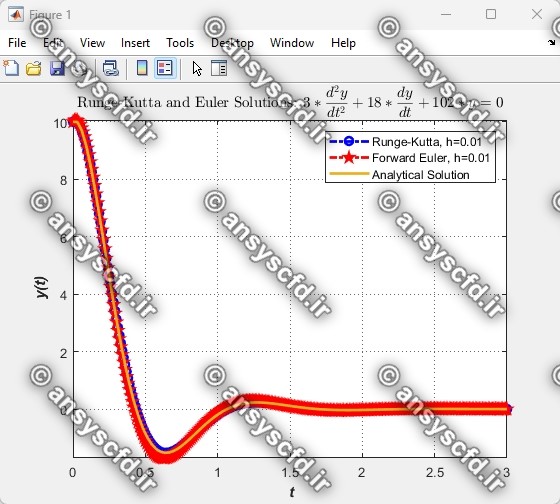
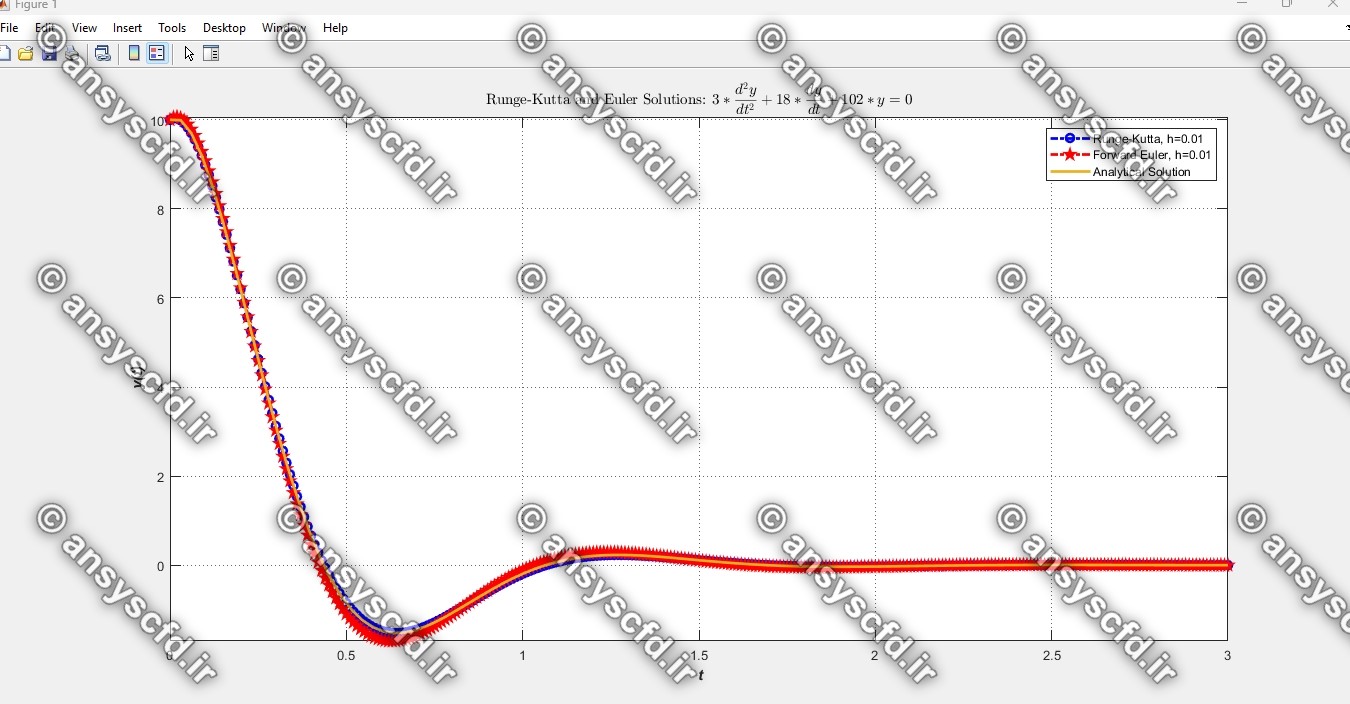
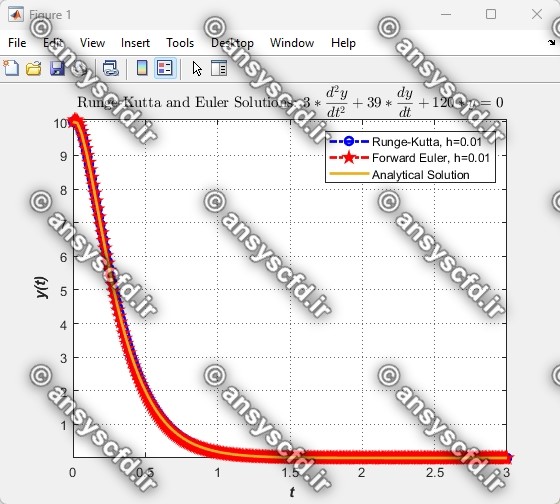
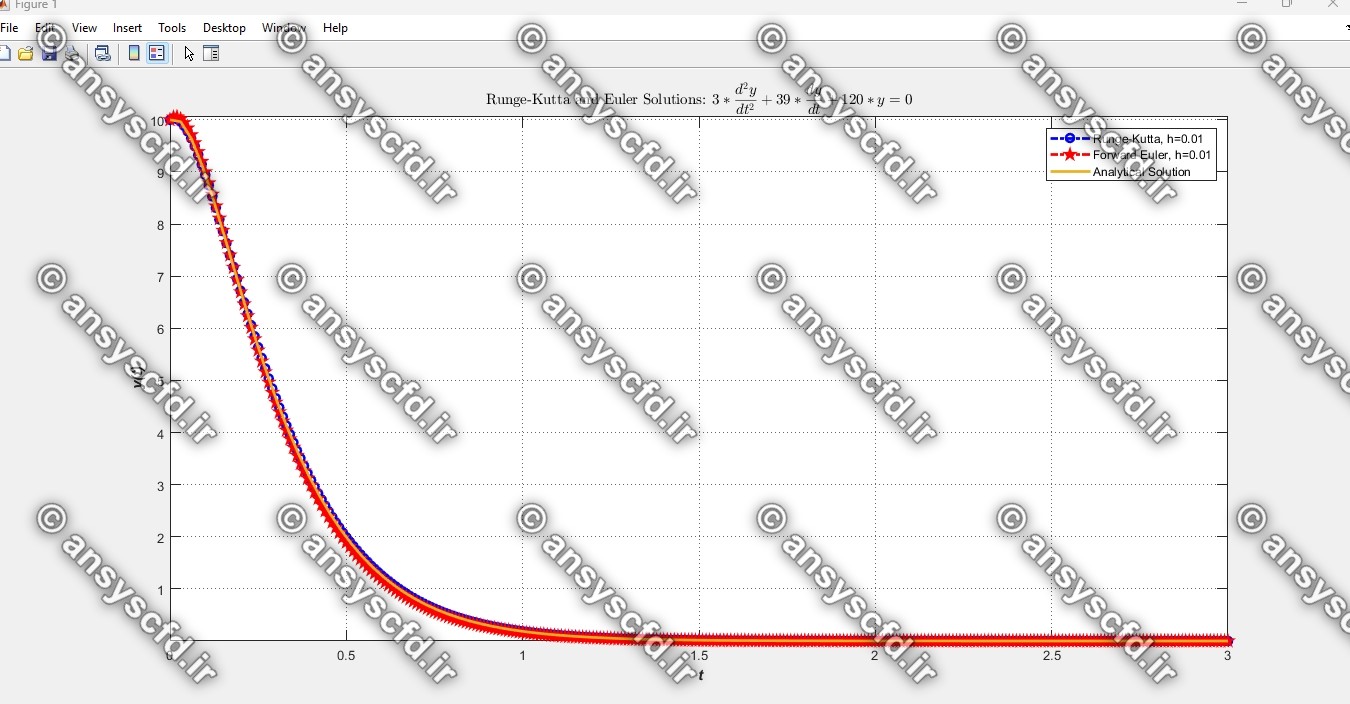
نتایج مقایسه روش اویلر و جواب تحلیلی: