توضیحات
حل معادلات دیفرانسیلی ارتعاشات آزاد و اجباری سیستم یک درجه آزادی(SDOF) جرم-فنر-دمپر با روش رانگ-کوتا مرتبه چهار(RK4) و روش اولر در نرم افزار متلب(MATLAB)
شرح پروژه:
در این پروژه حل معادلات دیفرانسیلی ارتعاشات آزاد و اجباری سیستم یک درجه آزادی(SDOF) جرم-فنر-دمپر با روش رانگ-کوتا مرتبه چهار(RK4) و روش اولر درنرم افزار متلب(MATLAB) کدنویسی شده است. در این پروژه علاوه بر کدهای متلب گزارش کامل فارسی پروژه را نیز دریافت خواهید کرد.
سیستم جرم-فنر-دمپر:
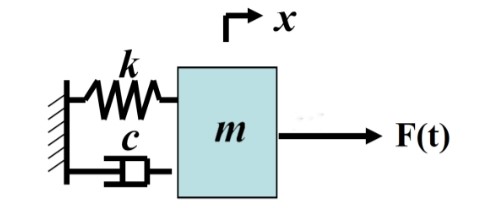
شکل-سیستم جرم-فنر-دمپر.
معادله دیفرانسیلی مرتبه دوم سیستم جرم-فنر-دمپر که دارای جرم m، ثابت فنریت k و ضریب میرایی c و x(t) جابجایی فنر (از نقطه تعادل خود) و f(t) نیروی خارجی یا ورودی سیستم است، به صورت زیر بیان می شود:
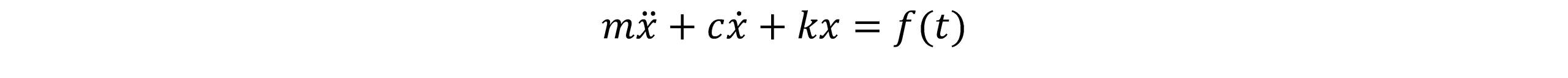
بازآرایی معادله دیفرانسیلی فوق به صورت زیر ارائه می شود:
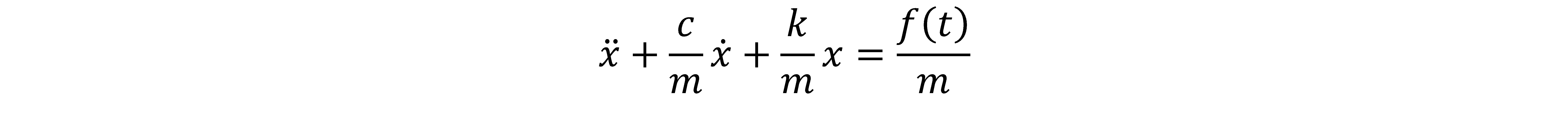
درصورتیکه نیروی خارجی صفر باشد معادله دیفرانسیلی فوق به صورت معادله دیفرانسیلی مرتبه دوم همگن بیان می شود:
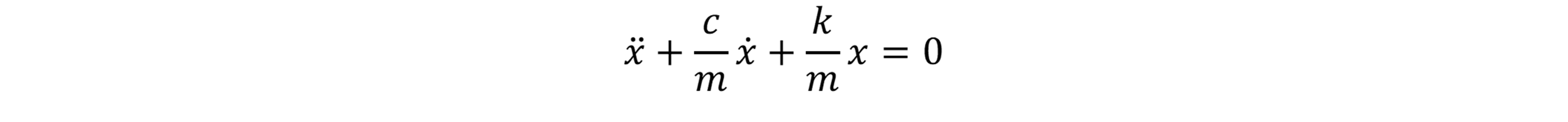
معادله فوق یک معادله دیفرانسیلی مرتبه دوم، خطی و همگن می باشد که شکل کلی جواب آن به صورت زیر بیان می شود.
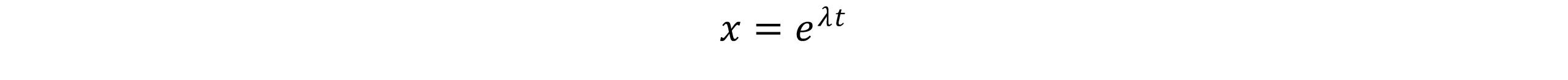
با قراردادن رابطه(4) در (3) معادله مشخصه بدست می آید:
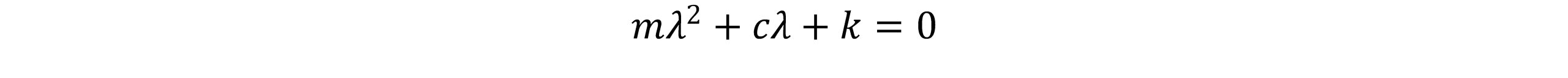
ریشه های معادله مشخصه بصورت زیر نوشته می شود:
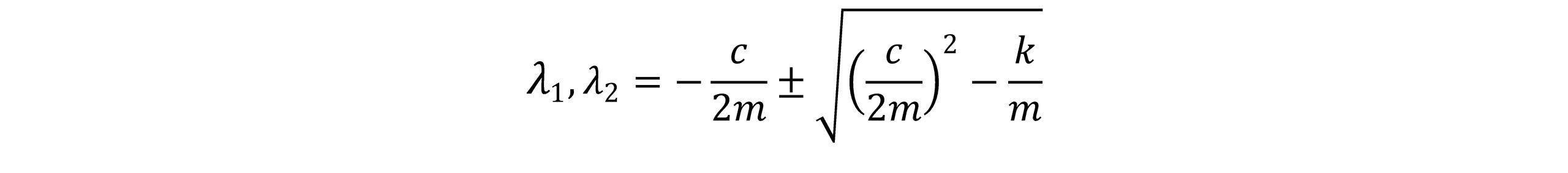
بنابراین جواب کلی معادله(3) مجموع دو تابع نمایی λ1 و λ2 می باشد.
ضریب میرایی بحرانی به صورت زیر بیان می شود:
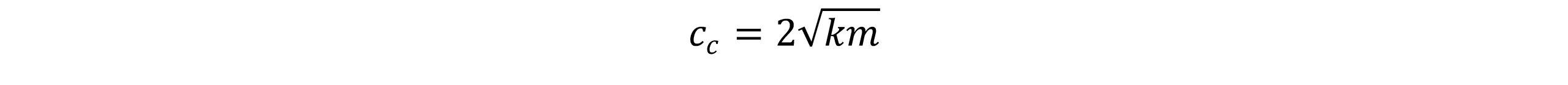
و ضریب میرایی(damping factor) به صورت نسبت زیر بیان می شود:
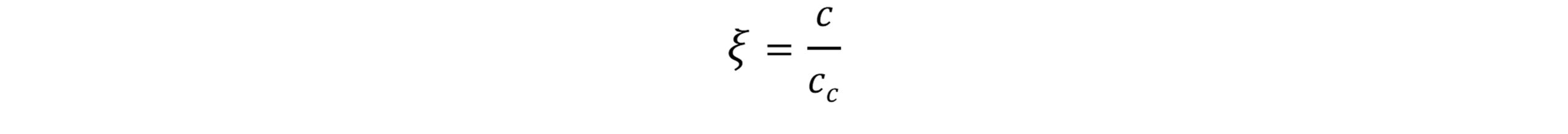
فرکانس طبیعی ارتعاش به صورت زیر بیان می شود:
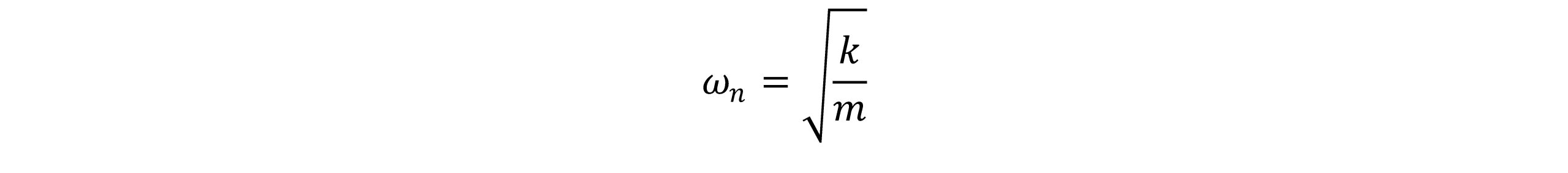
با قراردادن در λ1 و λ2 داریم:
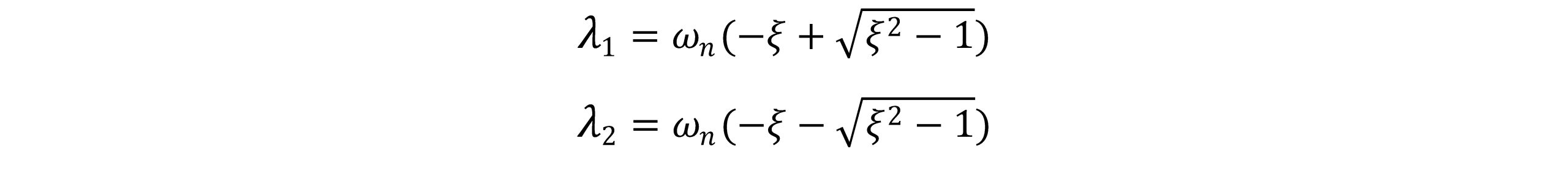
بنابراین جواب کلی معادله به صورت زیر بیان می شود:
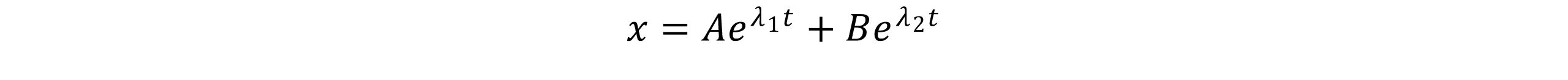
معادله فوق دارای سه حالت میرایی شدید، میرایی بحرانی و کم میرا می باشد که هر حالت بطور جداگانه بررسی می شود.
سیستم جرم-فنر-دمپر در حالت میرایی شدید(overdamped):
اینحالت زمانی بوجود می آید که میرایی بیشتر از میرایی بحرانی بوده و بنابراین نسبت میرایی بزرگتر از یک خواهد بود(c>cc و ξ>1)
در چنین حالت، ریشه های معادله مشخصه بصورت دو ریشه متمایز و حقیقی می باشند.
سیستم جرم-فنر-دمپر در حالت میرایی بحرانی(Critically damped):
اینحالت زمانی بوجود می آید که میرایی برابر میرایی بحرانی بوده و بنابراین نسبت میرایی برابر یک خواهد بود(c=cc و 1= ξ )
در چنین حالت، معادله مشخصه دارای دو ریشه تکراری می باشد.
سیستم جرم-فنر-دمپر در حالت کم میرا(Under damped):
اینحالت زمانی بوجود می آید که میرایی کمتر از میرایی بحرانی بوده و بنابراین نسبت میرایی کمتر از یک خواهد بود(c<cc و 1> ξ )
در چنین حالت، معادله مشخصه دارای دو ریشه مختلط می باشد.
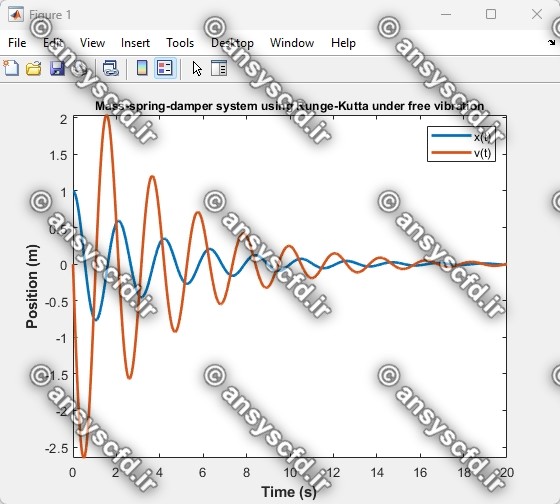
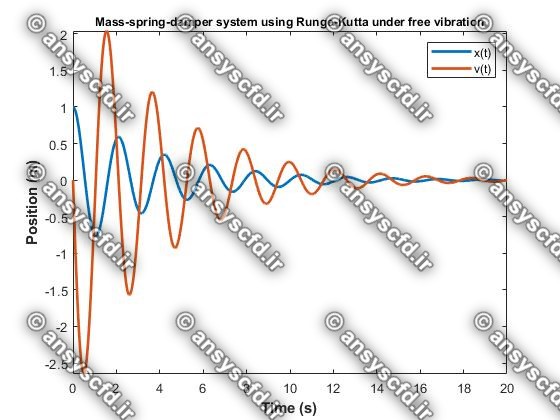
کدنویسی متلب روش رانگ-کوتا مرتبه چهار برای سیستم یک درجه آزادی جرم-فنر-دمپر در حالت ارتعاش آزاد:
کدنویسی متلب روش رانگ-کوتا مرتبه چهار برای سیستم یک درجه آزادی جرم-فنر-دمپر در حالت ارتعاش اجباری:
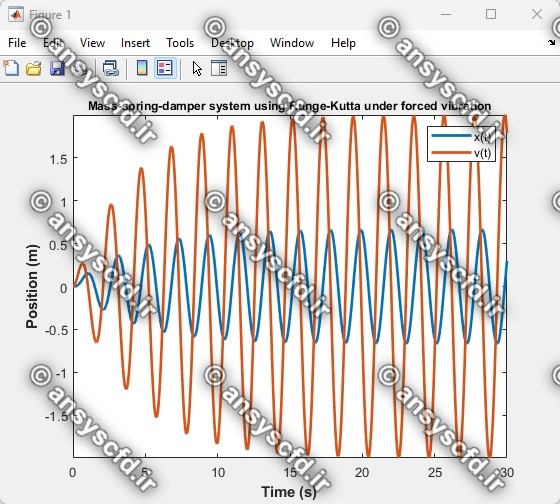
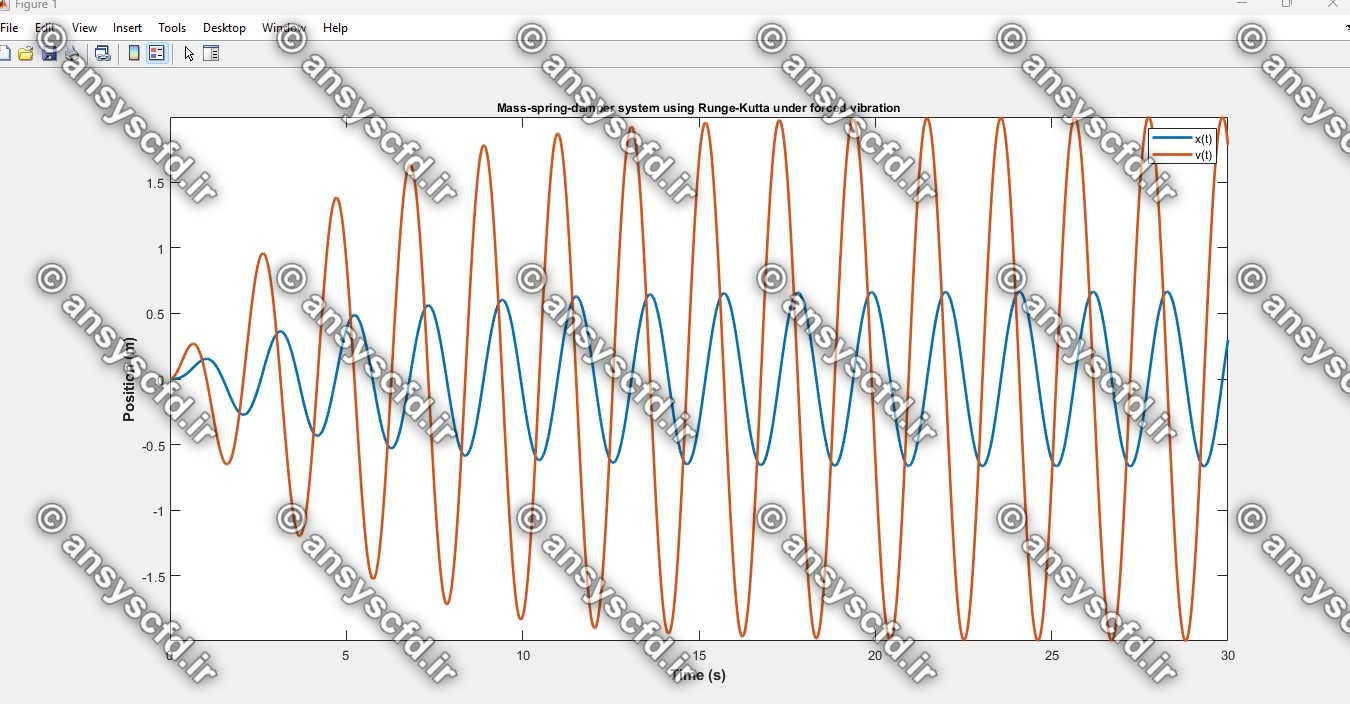
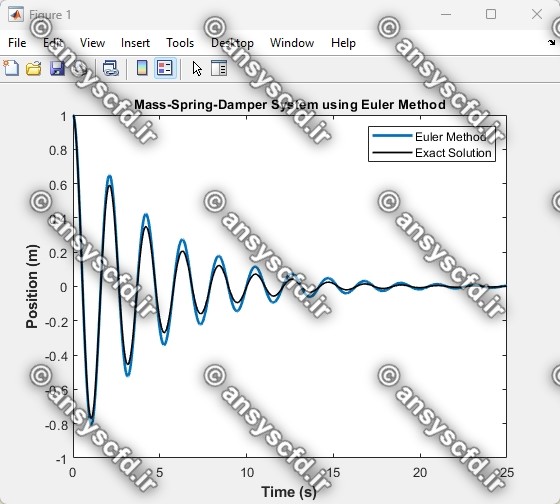
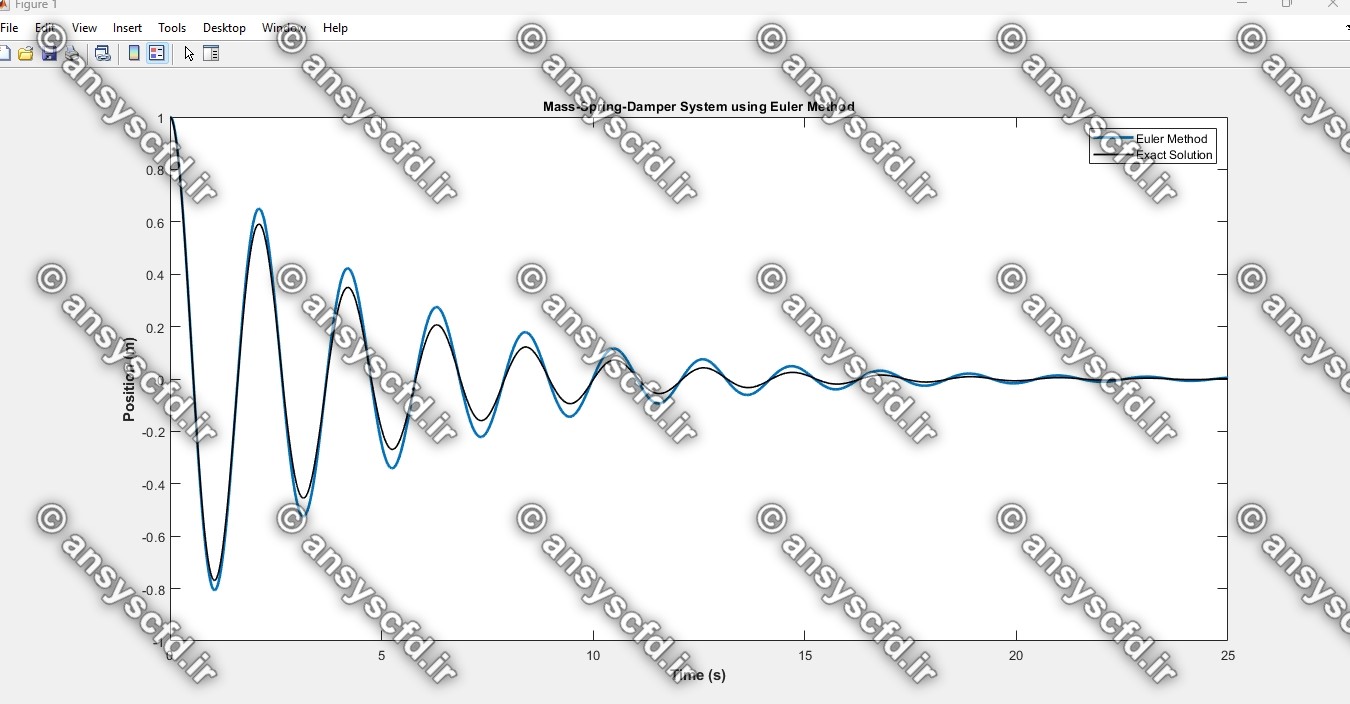
کدنویسی متلب روش اولر برای سیستم یک درجه آزادی جرم-فنر-دمپر در حالت ارتعاش آزاد: