توضیحات
پروژه برنامه نویسی عددی پدیده شکست سد با روش های عددی لکس وندروف(Lax-Wendroff)، گودونو(Godunov)، و ماسل( MUSCL ) در نرم افزار متلب
حل معادلات مربوط به شکست سد و در حالت کلی تر حل معادلات ناوير-استوکس سابقه ای نسبتا طولانی دارد و باتوجه به غیرخطی بودن و پیچیدگی این معادلات حل تحلیلی آنها به جز در حالت های خاص وجود ندارد. این امر باعث ارائه روش های متنوع توسط محققین جهت حل تقریبی این دسته معادلات، گردیده است. حل عددی این معادلات به دلیل وجود گرادیان های شدید، پیچیدگی های خاص دارد. با ورود کامپیوتر در عرصه علم و دانش و پیشرفت روز به روز این امر، رشد و گسترش روش های عددی در حل معادلات سرعت چشمگیری داشته است. جهت حل معادله شکست سد از سال ۱۹۸۰ تا ۱۹۹۰ روش های تفاضل محدود مختلفی برای معادلات با ناپیوستگی در دامنه جواب به کار گرفته شده است که کاربرد زیادی در حل جریانات کانال های باز دارد، از جمله این روش ها می توان به روش های ریمن توسط گلایستر (۱۹۹۸)، روش لكس – فردریش توسعه یافته توسط رائو، لاتا (۱۹۹۲) و نوجیک(۱۹۹۵) و روش گادانو توسط ساویک و هولی (۱۹۹۳) اشاره نمود. روش گادانو یک مرحله از روش بالادست، که خواص فیزیکی معادله جریان را در نظر می گیرد، جلوتر رفته و با استفاده از حل دقیق مساله ريمن، مشخصات فیزیکی بیشتری را در روش عددی در نظر می گیرد. در سالهای اخیر با توسعه ابزارهای محاسباتی برای حل معادلات دیفرانسیل و انتگرال، مطالعه شرایط پیچیده مثلا مقاومت جریان به کمک روش های عددی میسر شده است. بیش از چند دهه است که توسعه الگوریتم های عددی برای جریان ناشی از شکست سد بر بسترهای ثابت ادامه دارد. در این زمینه می توان از روش تفاضل محدود مرکزی و روش مک کورمک با شارهای پخشی مصنوعی، روش شار متکی به بالادست گودونو، حل کننده های تقریبی ریمن و روش کاهش تغییرات کل نام برد.
شکست سد:
شکست سد، رهایی ناگهانی آب ناشی از خرابی یا واژگونی سد است، که یکی از پرتلفات ترین فجایع انسانی می باشد. از جمله معروف ترین آنها می توان به شکست سد قوسی مالپاست فرانسه در تاریخ ۲ دسامبر ۱۹۵۹، به دلیل فشار روبه بالای آن اشاره نمود، و یا خرابی سد فرانسیس، که ساخت آن با ارتفاع 62.5 متر در ۷۲ کیلومتری لس آنجلس در سال ۱۹۲۶ به پایان رسید و آبگیری آن نیز در همان سال شروع شد. این سد ظرف مدت ۲ سال به بالاترین حجم مخزن خود یعنی 46.9 میلیون متر مکعب آب ذخیره شده در پشت سد رسید. با وجود بررسی های لازم در خصوص سلامت سد، این سد پس از ۵ روز از رسیدن به ماکزیمم حجم مخزن، به طور ناگهانی خراب شد. دلیل این واقعه ضعف بستر سد عنوان گردید.
تازه ترین شکست سدها در سال ۲۰۱۰ عبارتند از سد قز آقاش در قزاقستان، سد هاپ میلز کارولینای شمالی ایالات متحده، سد دلهی دو لووای ایالات متحده، سد آجكا آلومینا در مجارستان و سد کنمار در موزامبیک اشاره نمود. این پدیده را می توان با جریان های متغیر تدریجی و موج های پله ای (شاک) تشریح نمود. بروز پیاپی این اتقافات در چند دهه اخیر موجب شد تا محققین به بررسی جریان و امواج ناشی از شکست سد بپردازند. شکست سد نه تنها نشان دهنده ضعف مهندسی است بلکه یک تراژدی تلفات جانی بوده و بروز مشکلات سیاسی یک کشور را نیز می تواند به دنبال داشته باشد. عموما عامل اصلی شکست سدهای بتنی، مسائل مربوط به پی می باشد. فرسایش درونی پی و پدیده لانه روباه یا همان (Piping) باعث کاهش مقاومت برشی پی و درنتیجه واژگونی یا خرابی سد می گردد، عامل شکست سد مالپاست نیز همین دلیل عنوان شده است. در سدهای خاکی و بنایی نیز علاوه بر عامل مذکور، لبریزی از سد و فرسایش درونی بدنه بیشترین عوامل شکست گزارش شده است. عدم کفایت ظرفيت آبگذری سرریز از سد نیز از جمله عوامل گزارش شده در رابطه با شکست سد می باشد.
اهميت پدیده شکست سد:
با توجه به عظمت بنا، حجم بالای مصالح به کار رفته و هزینه های سنگین احداث سد، کارکرد اقتصادی و جنبه های تأمین نیرو و آب و ایجاد اشتغال، سد یک بنای استراتژیک محسوب می گردد که فروپاشی و انهدام آن، یک رویداد فاجعه بار است که ممکن است باعث خسارات جانی و مالی قابل توجه و آسیبهای زیست محیطی به علت خروج غیرقابل کنترل مقدار زیاد مخلوط آب و رسوب از مخزن شود که منجر به انتشار سیل مخرب و ویرانگر در پائین دست می شود؛ بنابراین تمامی تلاش محققین و دانشمندان به بررسی همه جانبه و محدود ساختن ابعاد خسارات ناشی از شکست سد می باشد. انتظار می رود که پیشرفت های مساعد در طراحی سد و تکنیک های ساخت آن، منجر به کاهش حوادث شکست شود. با این حال به دو دلیل اصلی مسئله شکست سد اتفاق می افتد اول اینکه با هر پیشرفت تکنولوژی، همیشه به احتمال زیاد عوامل پیش بینی نشده ای وجود دارد که می تواند مسائل و مشکلات غیرمنتظره ای را ایجاد کند. و دومأ بسیاری از محل های مناسب برای سد، در سراسر جهان استفاده شده اند؛ این به این معنا است که ساخت سدهای آینده، در محل های بسیار مشکل و پیچیده زمین شناسی، ضروری خواهد بود که باعث افزایش احتمال وقوع شکست سد می شود؛ بنابراین واضح است که اگر بخواهیم شکست سد و حوادث آن در آینده به حداقل برسد، باید نقش پیشرفت تکنولوژی در هنگام تحقیق و بررسی، طراحی و ساخت وساز سد افزایش یابد. مسائل و مشکلات سد معمولا به صورت ترمهای قابل مقایسه و طبقه بندی شده بیان نمی شوند و این می تواند گاهی اوقات باعث فهم نادرست شود. شکست سد به صورت زیر تعریف شده است «فروپاشی یا جابه جایی قسمتی از سد یا فونداسیون آن، به طوری که سد نمی تواند آب را نگه دارد. به طور کلی شکست سد منجر به آزاد شدن مقدار زیادی آب می شود که خطرات زیادی را برای مردم و یا اموال پائین دست اعمال می کند».
هیدرولوژی و هیدرولیک شکست سد از موضوعاتی هستند که در زمینه های برنامه ریزی منابع آب، حفاظت محیط زیست و مدیریت بوم شناسی با توجه به پتانسیل وقوع حوادث شدید هواشناسی ناشی از تغییرات آب و هوایی و حوادث طبیعی تاریخچه شکست سد، موجب افزایش علاقه شده اند. پیش بینی شکل، اندازه و زمان جاری شدن سیل ناشی از شکست سد، برای برنامه ریزی تخلیه و ایمنی مدیریت عملکرد مخزن مهم است.
شکست سدهای معروف:
سدها توسط مهندسین زیادی ساخته شدند؛ با این ادعا که این ساختمانها برای برجا ماندن برای قرنها ساخته شده اند. با این حال سدها بارها و بارها فروریختند و برخی از آنها منجر به حوادث فاجعه بار بزرگی شدند.
شکست سد بانكیاوا و سد مخزنی شیمانتان – چین (۱۹۷۵):
سد بانکیاو در سال ۱۹۵۲ بر روی رودخانه هوایی در استان هنان چین ساخته شد. این سد، نیرویی در حدود ۱۸ گیگاوات الكتریسیته را برای این ناحیه تأمین می کرد. بعد از پایان مراحل اولیه ساخت، ترکهایی در بدنه سد دیده شد که با توصیه های مشاوران روسی تعمیر شده و این سد به عنوان سدی پایدار به نام «سد آهنین» مشهور شد. این سد برای مقاومت در برابر بارش ۳۰ میلی متر در روز، اتفاقی که در هر ۱۰۰۰ سال در آن ناحیه رخ میدهد ساخته شده بود. اما در آگوست سال ۱۹۷۵ میلادی در اثر طوفان نینا باعث شد که در عرض ۲۴ ساعت۱۰۶۰ میلیمتر باران ببارد. به دلیل وقوع طوفان، سیستم های ارتباطی نابود شده و باعث شد که درخواست باز کردن دریچه های سد به موقع به واحدهای مهندسی نرسد. تراز آب در سد شروع به افزایش و بالا آمدن کرد تا جایی که دریچه های رسوب قادر به کنترل تمام فشار آب نبودند و باعث ویرانی سریع دریچه ها شد. در نتیجه، در مجموع 1.7 میلیون مترمکعب آب با سرعت متوسط ۳۱ مایل در ساعت آزاد شد که حتی زمین های واقع شده در هزاران کیلومترمربع دورتر از آن را ویران کرد. شمار کشته شدگان در این حادثه ۱۷۱۰۰۰ بوده است.

شکل شکست سد بانكیاو چین-۱۹۷۵.
شکست سد وایونت – ایتالیا (۱۹۶۳):
این سد واقع در دره رودخانه وایونت می باشد که در میان بلندترین سدهای جهان می باشد. اگرچه امروزه از این سد استفاده نمی شود، ولی هنوز هم به بهترین شکل خودش به عنوان اینکه هرگز از نظر ساختاری ویران نشده است، پابرجا است. منطقه اغلب توسط زمین لرزه های جزئی آسیب دیده است ولی هرگز بر روی سد تأثیری نگذاشته است. در اکتبر ۱۹۶۳، درحالی که مخزن در حال پر شدن با آب بود، زلزله به منطقه آسیب رساند و در اثر رانش، خاکریزه ای در حدود ۲۶۰ میلیون مترمکعب در داخل مخزن فروریخت. تنها در عرض۴۵ ثانیه کل منطقه در آب غوطه ور شد و در حدود ۵۰ میلیون مترمکعب آب از سد به صورت امواج با ارتفاع ۲۵۰ متر آزاد شد که به طور کامل روستاهای اطرافش را ویران کرد و در حدود ۲۰۰۰ نفر کشته شدند.

شکل شکست سد وایونت ایتالیا – ۱۹۶۳.
شکست سد مالپاست- فرانسه (۱۹۵۹):
سد مالپاست بر روی رودخانه ری ران واقع در ریورا فرانسه در قسمت جنوبی فرانسه ساخته شد. در سال ۱۹۵۹، صداهای ترک در نزدیکی دیوارهای سد شنیده می شد اما به دلیل عدم توانایی فنی، نتوانستند آن را بررسی کنند. در نهایت سد در ۲ سپتامبر ۱۹۵۹ شکسته شد و تمام دیوارهای آن به صورت قطعاتی فروریخت. امواج با بیش از ۴۰ متر ارتفاع شروع به عبور از مناطق مجاور کردند که باعث تلفات سنگینی به سازه ها شد. شمار کشته شدگان در این حادثه۴۲۳ نفر اعلام شد. به طور کلی، دلایل تخریب سد مالپاست را به صورت زیر طبقه بندی کردند: 1. افزایش نسبی فشار آب در توده سنگی و ایجاد ترک و شکاف در بالادست سد. ۲. بازشدگی ترک ها در طول پاشنه سد در مدت ۱ سال و سرانجام جابجایی پیش رونده پای سد و دوران پوسته سد حول تاج. ٣. وجود شرایط خطرناک (مانند گسل) اساسأ در جناح چپ سد. 4. در جابجایی های سریع در لحظه گسیختگی، این مقدار در امتداد رودخانه افزایش یافته و در نهایت به علت دوران سد در دو امتداد و بیرون زدن توده سنگ در پایه چپ سد، كل پوسته تخریب شده است.

شکل شکست سد مالپاست فرانسه – ۱۹۵۹.
روش های حل معادلات آبهای کم عمق:
معادلات دیفرانسیل جزئی آب های کم عمق به سادگی قابل حل نبوده و راه حل تحلیلی مشخصی نیز برای آنها وجود ندارد. گاه برای حل آنها از روش های تقریبی فرضیاتی نسبت به وضعیت جریان استفاده می گردد. بدیهی است هرچه فرضیات جهت ساده کردن معادلات و حل تحلیلی آنها به واقعیت امر نزدیکتر باشد، جواب ها از خطای کمتری برخوردار خواهند بود. یکی از روشهایی که امروزه در حل این معادلات جزئی کاربرد زیادی دارد روش های عددی می باشد.
روش های عددی:
حل معادلات آبهای کم عمق به روش تحلیلی تنها در حالات بسیار خاص و محدودی از امواج امکانپذیر است، در این حالت باید بتوان معادلات مذکور را با فرضیاتی ساده نمود. استفاده از روش های ترسیمی نیز زمان بر است و کمتر مورد توجه قرار می گیرد، از طرف دیگر گسترش و توسعه ی کامپیوترها و استفاده از سرعت های بالای آنها در حل معادلات پیچیده، روش های عددی کم کم جای سایر روش ها را گرفته و به خصوص امکان اعمال عوامل و شرایط بیشتر و از طرفی همزمان با آن، دسترسی به نتایج و جواب های نسبتاً دقیق، باعث شده تا روش های دیگر کم کم به فراموشی سپرده شوند. برای حل معادلات آب های کم عمق به روش عددی، تکنیک های مختلفی وجود دارد که هریک از نقطه نظر همگرایی، ثبات، دقت و راندمان، امتیازات مخصوص به خود را دارند.
در روش مشخصه ها معادلات پیوستگی و اندازه حرکت به دو جفت معادلات دیفرانسیل معمولی که مشخصات و خصوصیات جریان را مشخص می نمایند، تبدیل گشته و سپس از طریق روش تفاضل محدود حل می گردند. در روش تفاضل محدود با روش مستقیم، مشتقات جزئی با تفاضل محدود تعویض شده و معادلات جبری حاصله حل می گردند. برای استفاده از روش اجزای محدود، سیستم به تعدادی جزء کوچک تقسیم شده و از معادلات دیفرانسیل جزئی در گرههای مربوط به هر جزء انتگرال گرفته می شود. معادلات تفاضل محدود تخمین هایی بر معادلات دیفرانسیل هستند. بیشتر عبارات تفاضل محدود با استفاده از بسط سری تیلور نوشته می شوند. استفاده از روش های عددی در موضوعات گوناگون علمی، از دیرباز مطرح بوده است. اما پیشرفتهای به دست آمده در امر ساخت و بهبود کامپیوترها که موجب افزایش کارآیی و حافظه آنها گردیده، امکان حل معادلات مکانیک سیالات با استفاده از روش های عددی مختلف را بیش از پیش مطرح ساخته است. این پیشرفت ها سبب معرفی روشهای عددی جدیدتری شده اند که تقریبا به صورت روزانه پیشنهاد می شوند. همچنین انعطاف پذیری این روش ها جهت در نظر گرفتن ابعاد گوناگون مسائل مورد بحث و امکان بررسی همه جانبه و دقیق شرایط و جزئیات یک معادله حاکم سیالاتی، موجب شده تا اهداف پیش بینی شده در حل یک مساله سیالاتی توسط این روش ها به خوبی برآورده گردد. با مقایسه جوابهای حاصله از روش های عددی گوناگون، خواه از نوع تفاضل محدود و خواه از نوع روش های حجم محدود، با نتایج آزمایشگاهی، می توان صحت و سقم و معایب و مزایای انواع این روش ها را مورد بررسی و نقد دقیق قرار داد و نسبت به کارآیی یا عدم کارآیی یک روش عددی جهت مقاصد عملی نظر داد.
روش عددی گودونو(Godunov):
یکی از روش های شناخته شده و مطرح در حوزه روش های احجام محدود روش عددی گودونو می باشد که نام آن برگرفته از نام گودونو، محققی است که در سال ۱۹۵۹ آن را ابداع نمود. این روش حجم محدود جهت حل سیستم هایی که معادلات حاکم آنان از نوع هذلولوی می باشند کاربرد دارد. انگیزه گودونو از ابداع این این روش، وجود برخی محدودیت های روش مشخصه بود. اما با وجود اینکه روش عددی گودونو در اواخر دهه ۱۹۵۰ پا به عرصه وجود نهاد، اما در آن زمان حتی نتوانست به شهرت و رواج برخی روشهای عددی برسد که در سال های بعد توسعه داده شده و از روش گودونو کارآیی و توانمندی کمتری داشتند. دو دلیل عمده این مساله را باید در درجه نخست، در ماهیت صریح بودن این روش جستجو نمود، چرا که این مساله باعث اعمال نوعی محدودیت در گام زمانی محاسباتی به منظور برقراری شرط پایداری در مساله می شد. این در حالی است که در دهه های ۱۹۶۰ و ۱۹۷۰ میلادی، غالبا فرمولبندی های ضمنی ترجیح داده می شدند. زیرا این روش ها اجازه انتخاب گام زمانی بزرگتری را می دادند، بی آنکه باعث بروز ناپایداری در مساله شوند. ثانيا در این روش، گودونو، برای محاسبه شارها و تبادل بین آنها در مرزهای سلولهای محاسباتی از پروسه ای تحت عناون مسائل ریمان سود برد. این در حالی است که حل مسائل ریمانی به عنوان یکی از عمده ترین بخشهای روش عددی گودونو تا مدتها به عنوان فرآیندی هزینه بر و اتلاف کننده از نظر زمانی، تلقی میشد و سرانجام با ظهور روش های حل تقریبی مسائل ریمان در دهه ۱۹۸۰، یک ابزار قوی و کارآمد برای حل مسائل ریمان ایجاد شد. در کنار این روشهای تقریبی، با افزایش سرعت و دقت کامپیوترها، امکان حل دقیق مسائل ریمانی نیز با سرعت بیشتری نسبت به قبل فراهم شد و همه این عوامل مجددأ باعث جلب توجهات به روش عددی گودونو گردید. در سه دهه اخیر، با پیشرفت ساختار روش عددی گودونو و ابداع فرمهای گوناگونی از این روش جهت بررسی حالات مختلف مورد مواجهه از قبیل مسائل غیر خطی و خطی، روش های گوناگون حل مسائل ریمان و … انواع مختلفی از روش های صریح شکل گرفتند که پایه و اساس همگی آنان ساختاری بود که گودونو در سال ۱۹۵۹ ابداع نمود. امروزه روش عددی گودونو به موازات سایر روشهای عددی، در رقابتی تنگاتنگ برای مدلسازی مسائل مختلف حضور دارد. هرچند از آن زمان تا کنون استفاده از روش عددی گودونو در حوزه های مختلف سیالاتی و فیزیکی و.. جهت مدلسازی معادلات دیفرانسیل هذلولوی، بارها و بارها تکرار شده است و قابلیت این روش در موارد گوناگون مورد بحث و بررسی قرار گرفته است.
روش لکس وندروف:
روش لکس-وندروف یک روش برپایه تقریب تفاضلات متناهی است. که توسط لکس و وندروف تعریف شده است. این روش براساس بسط تیلور بدست آمده است.
روش الگوی یکنوای بالادست برای قوانین پایستار(MSUCL):
الگوی یکنوای بالا دست برای قوانین پایدار(MSUCL) اولین بار توسط ون لیر پیشنهاد شد. براساس این روش در مرحله موسوم به بازساخت داده ها، مقادیر متغیرها در مرز سلول با برون یابی مقادیر مرکز سلول به دست می آیند. اعمال این برون یابی به گونه ای صورت می پذیرد که خصلت نوسانی جواب کنترل شود و ناپیوستگی های جریان بدون ایجاد استهلاک عددی تسخیر شود. برای بازساخت داده ها از یک محدودکننده غیر خطی شیب استفاده می شود تا استهلاک عددی مناسب به داده های بازسازی شده در مرز سلول افزوده شود. با استفاده از این روش، ضمن حفظ یکنوایی حل، از ایجاد نوسان های شدید و غیر فیزیکی در نزدیکی نواحی با گرادیان زیاد جلوگیری می شود.
شرح پروژه:
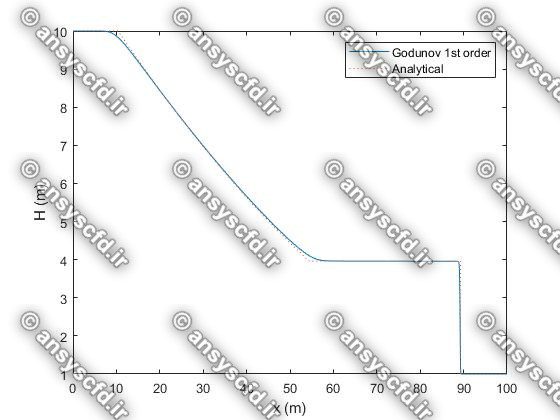
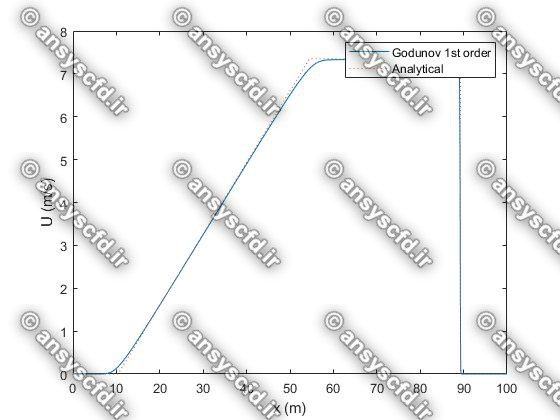
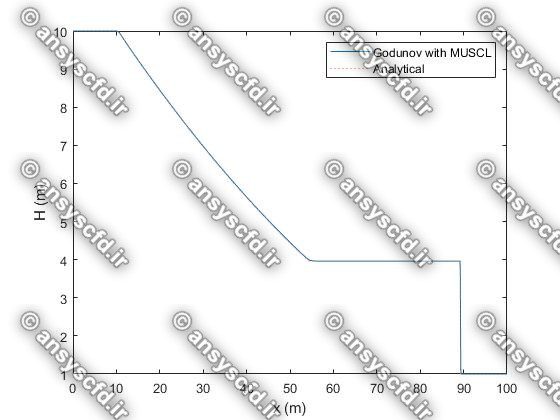
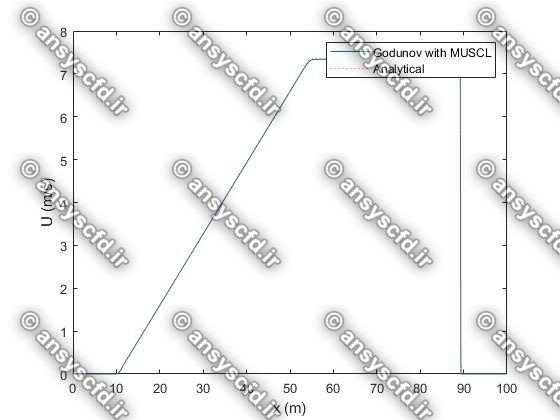
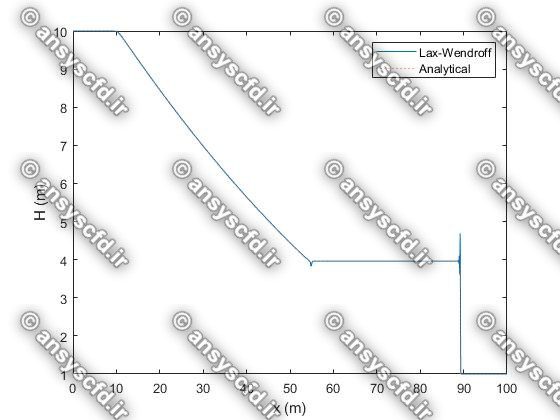
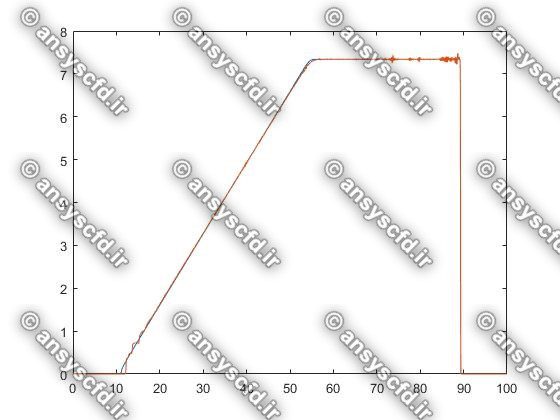
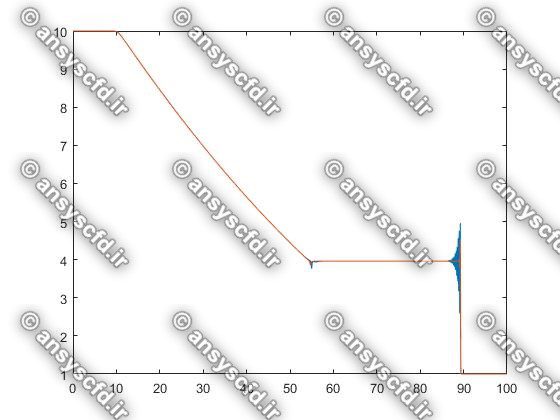
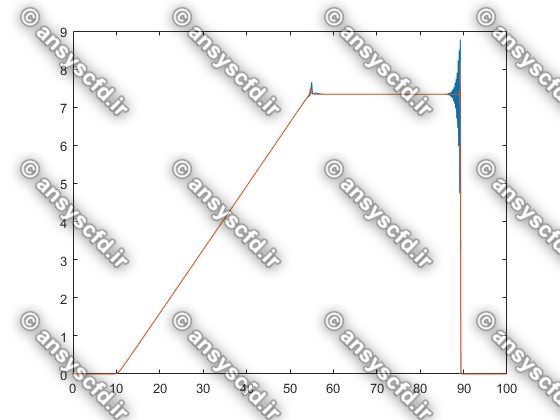
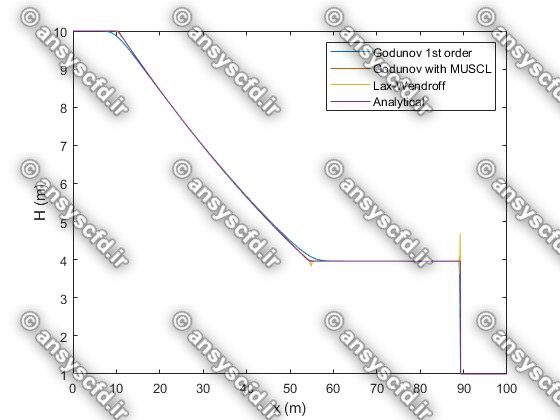
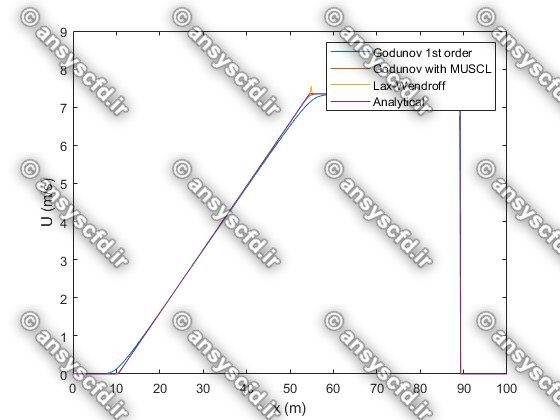
در این پروژه برنامه نویسی عددی پدیده شکست سد با روش های عددی لکس وندروف(Lax-Wendroff)، گودونو(Godunov)، و ماسل( MUSCL ) در نرم افزار متلب انجام شده است.
نمونه نتایج: