توضیحات
پروژه متلب حل معادلات فضای حالت مدار RLC سری با روش ODE45
مدارهای RLC:
در الکترونیک(خازن؛ سلف؛ مقاومت)؛ که به ترتیب با نمادهای C , L , R نشان داده میشوند، سه عنصر غیرفعال الکترونیکی(چون نیروی محرکهای در درون خود ندارند) هستند که معمولا در مدارهای الکترونیکی به اشکال مختلف به یکدیگر وصل میشوند. کلیترین حالت زمانی است که هر سه عنصر در یک مدار وجود داشته باشند. این حالت را اصطلاحاً مدار RLC میگویند.
در الکترونیک برای تحلیل مدار RLC ابتدا مدار را با شرایط اولیه عناصر ذخیرهکننده انرژی در نظر میگیریم. اگرچه ممکن است این مدارها شامل منابع وابسته باشند، اما بدون منابع مستقل هستند. مدارهای بدون منبع، دارای پاسخ طبیعی هستند. عموماً مدار RLC موازی را با حضور منابع مستقل بررسی میکنیم که در این صورت، هم پاسخ گذرا و هم ماندگار خواهد داشت. مدارهای RLC موازی، در بسیاری از کاربردها عملی مانند شبکههای مخابراتی و طراحی فیلتر بهکار میروند.
مدارهای الکترونیکی:
مدارهای الکترونیکی از اجزای مختلفی تشکیل شدهاند که به هم متصل شده و یک مدار بسته کامل را میسازند. سه عنصر پسیو یا غیرفعال (Passive Component) اصلی هر مدار، مقاومت (Resistor)، خازن (Capacitor) و سلف (Inductor) هستند. همه این اجزای پسیو، یک ویژگی مشترک دارند و آن این است که در برابر جریان الکتریکی مدار مقاومت میکنند و آن را محدود میسازند.
جریان الکتریکی به دو صورت در مدار گردش میکند. اگر جریان فقط در یک جهت گردش کند، بهعنوان جریان مستقیم(DC) شناخته میشود و اگر در دو جهت(مثبت و منفی برای یک عنصر) گردش کند، جریان متناوب(AC) نامیده میشود. اگرچه عناصر پسیو در مدارهای AC دارای امپدانس هستند، اما رفتاری بسیار متفاوت از حضورشان در مدارهای DC را به نمایش میگذارند.
اجزای پسیو، انرژی الکتریکی مصرف میکنند و میتوان آنها را به صورتهای مختلف در مدارهای الکتریکی و الکترونیکی بهکار برد.
مقاومتها، در مدارهای DC و AC، مقدار مقاومت (Resistance) الکتریکی یکسانی دارند که مستقل از فرکانس منبع است. این، به آن دلیل است که مقاومتها عناصر خالصی هستند و ویژگیهای پارازیتی خاصی از قبیل ظرفیت (Capacitance) بینهایت (C=∞) و اندوکتانس (Inductance) صفر( (L=0دارند. در یک مدار مقاومتی، ولتاژ و جریان همیشه هم فاز بوده و توان مصرف شده در هر لحظه، با ضرب ولتاژ در جریان همان لحظه بهدست میآید. از سوی دیگر، خازنها و سلفها، نوع دیگری از مقاومت را در مدارهای AC نشان میدهند که راکتانس (Reactance) نامیده میشود(XL و XC) راکتانس نیز در برابر عبور جریان مقاومت میکند، اما مقدار راکتانس یک سلف یا خازن، مانند یک مقاومت ثابت نیست و به فرکانس منبع و مقدار آن در حالت DC بستگی دارد.
عناصر پسیو در مدارهای AC، بهدلیل تاثیر فرکانس (f)، بسیار متفاوت از حالتی عمل میکنند که در مدارهای DC قرار دارند. در یک مدار مقاومتی خالص، جریان با ولتاژ همفاز بوده، اما در یک مدار خازنی خالص، جریان خازن 90 درجه از ولتاژ آن جلوتر است و در یک مدار سلفی خالص، جریان به اندازه 90 درجه از ولتاژ عقبتر خواهد بود.
مخالفت با عبور جریان در یک مدار AC، برای یک مقاومت (Resistor)، مقاومت (Resistance) یا R نامیده میشود. مقدار این مخالفت با گذر جریان، برای یک خازن، راکتانس خازنی (XC) و برای یک سلف، راکتانس سلفی یا القایی (XL) است. ترکیب مقاومت و راکتانس، امپدانس (Impedance) نامیده میشود.
در مدارهای سری، مجموع فازوری ولتاژ عناصر مدار برابر با ولتاژ منبع تغذیه VS است. در یک مدار موازی، مجموع فازوری جریان گذرنده از شاخهها و درنتیجه عناصر، برابر با جریان منبع( IS) است.
در مدارهای RLC سری و موازی، وقتی جریان منبع، با ولتاژ منبع هم فاز باشد و XL=XC، پدیدهای بهنام «تشدید» یا رزونانس (Resonance) رخ میدهد. مدار تشدید سری، مدار پذیرنده (Acceptor Circuit) و تشدید موازی، مدار دفعکننده (Rejecter Circuit) نامیده میشوند.
شرح پروژه:
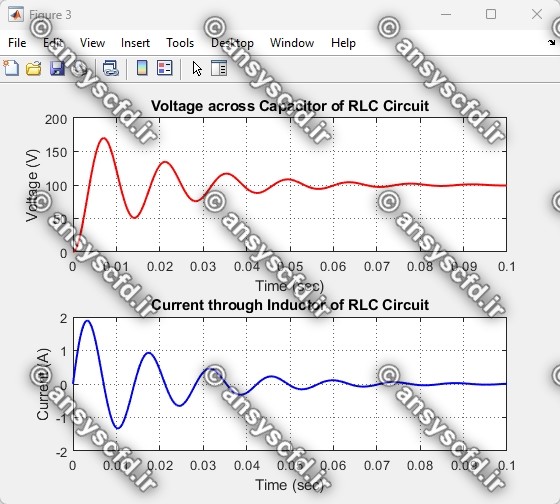
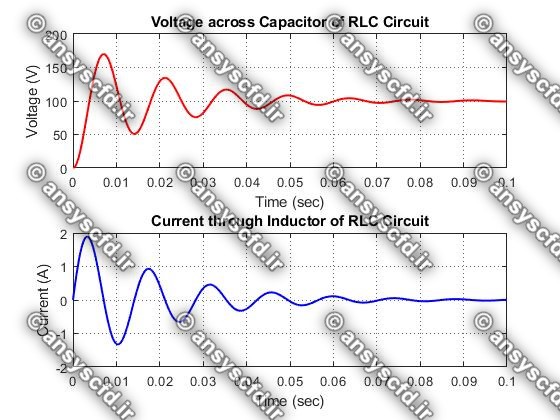
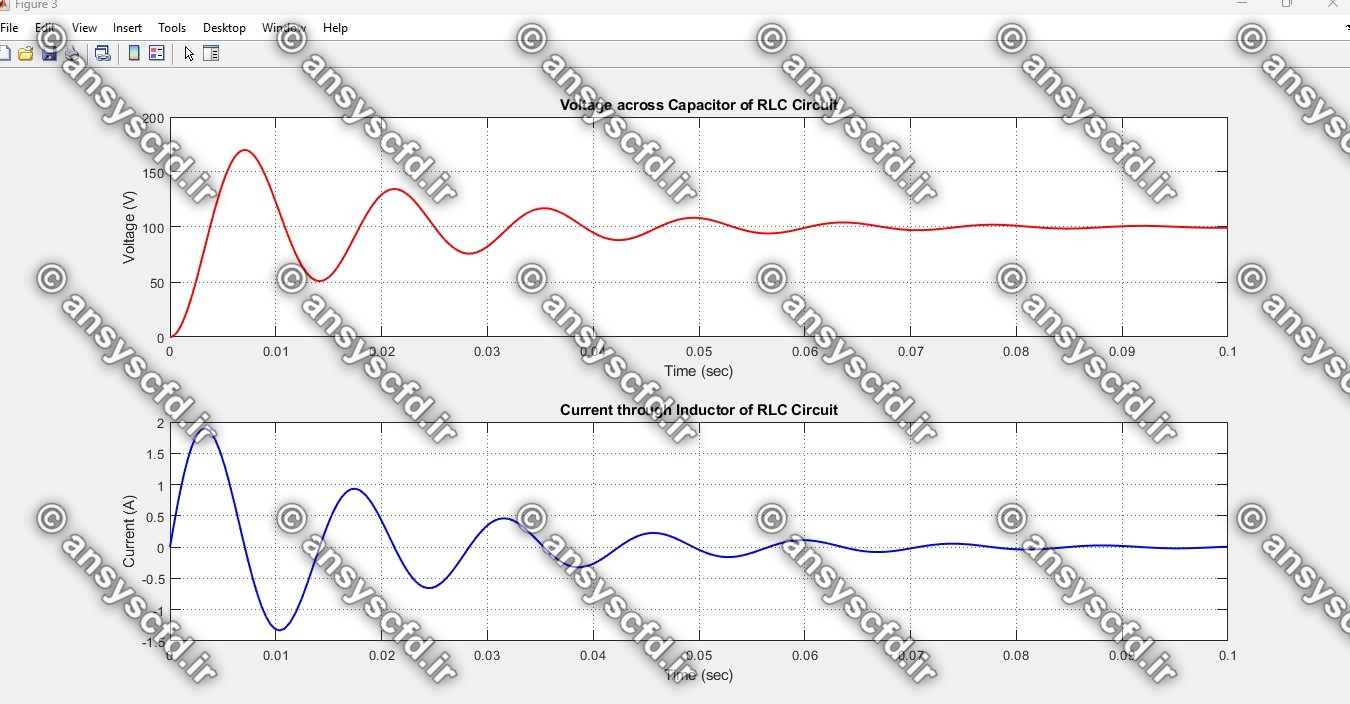
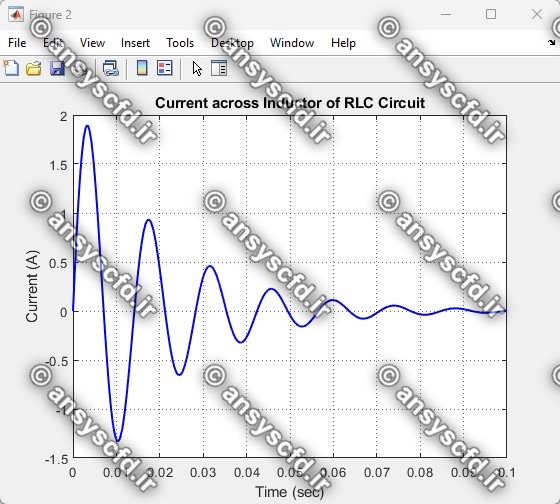
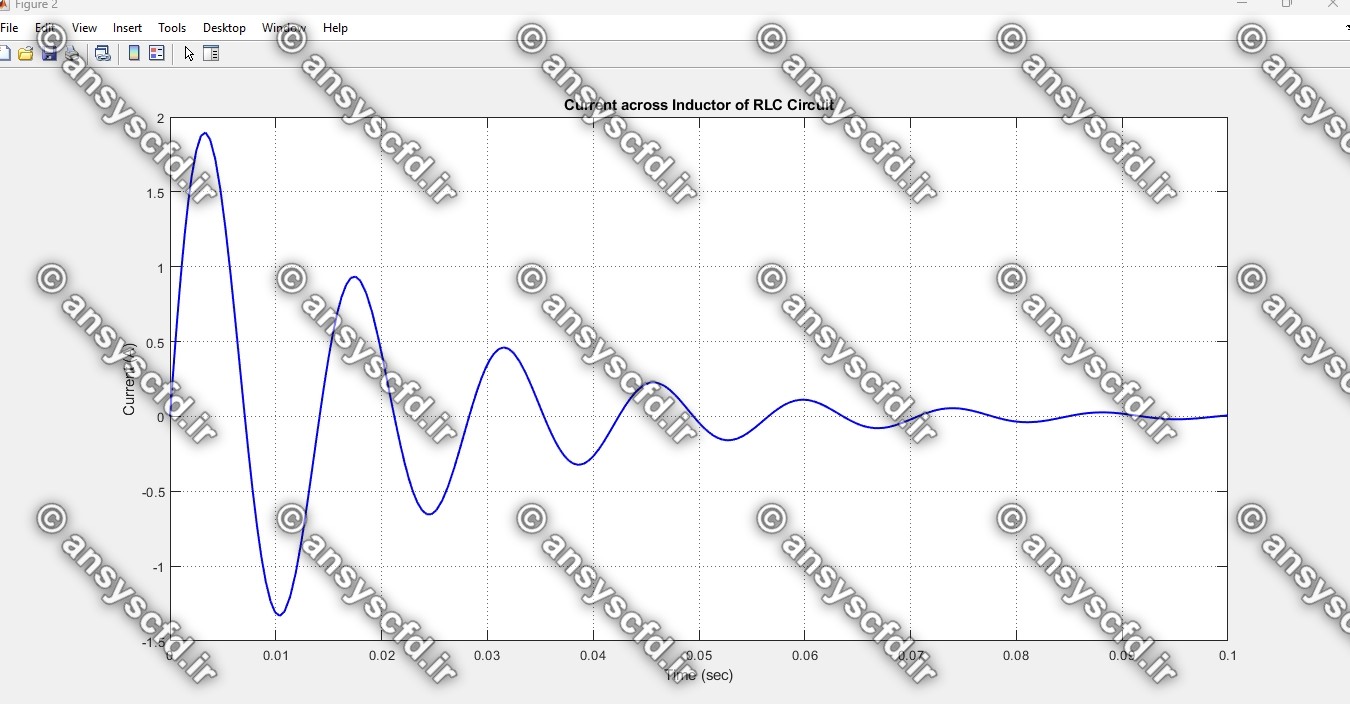
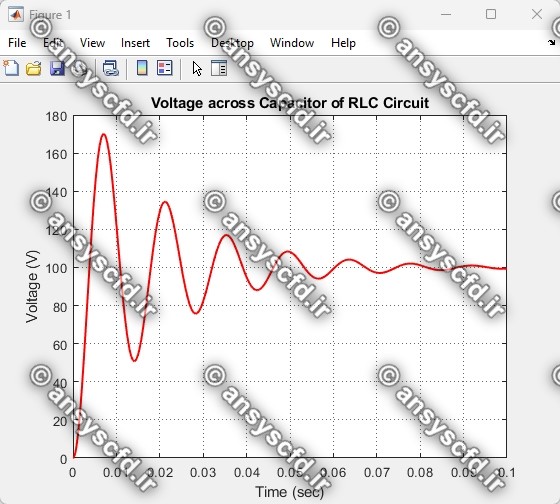
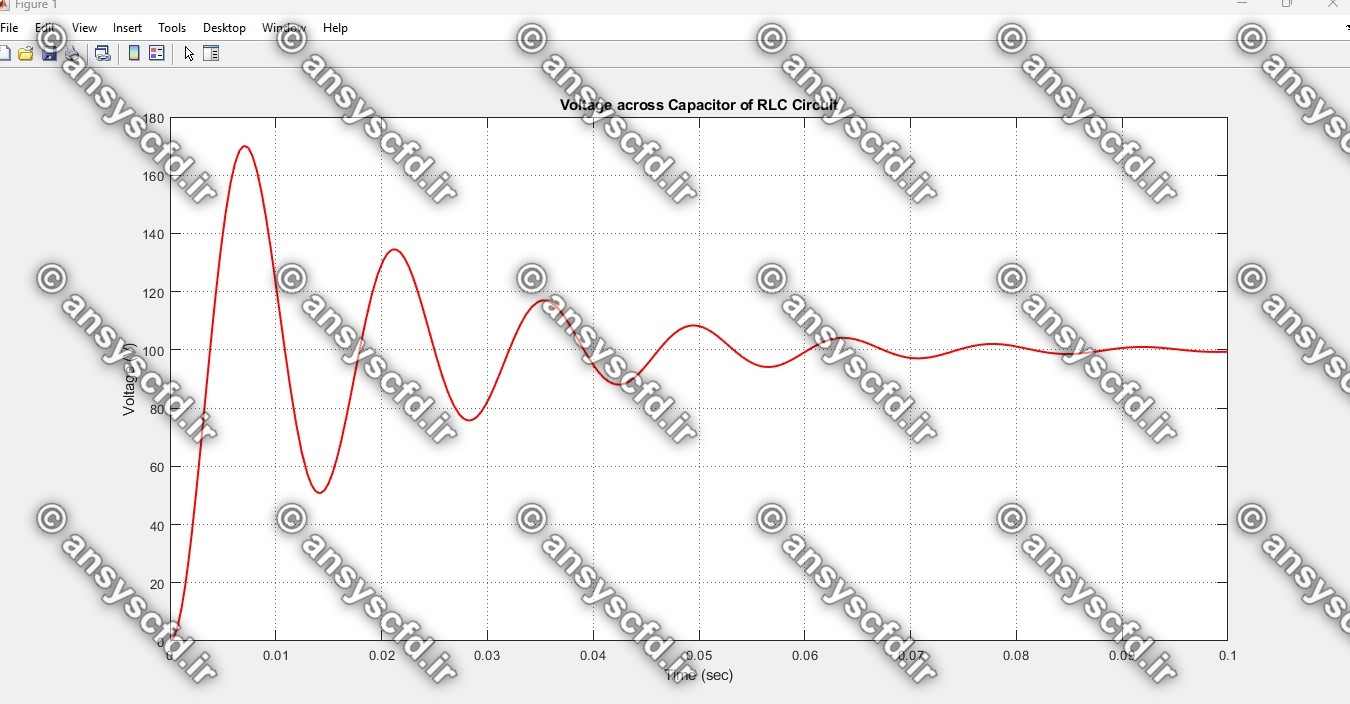
در این پروژه معادلات فضای حالت(state space) مدار RLC با روش ODE45 در متلب کدنویسی شده است. و نمودارهای ولتاژ دو سر خازن و جریان برحسب زمان نمایش داده شده است.
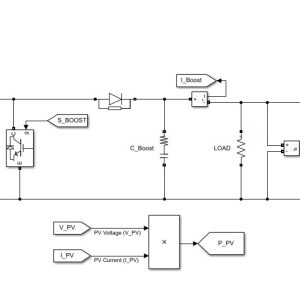
مدار RLC سری مطابق شکل زیر می باشد:
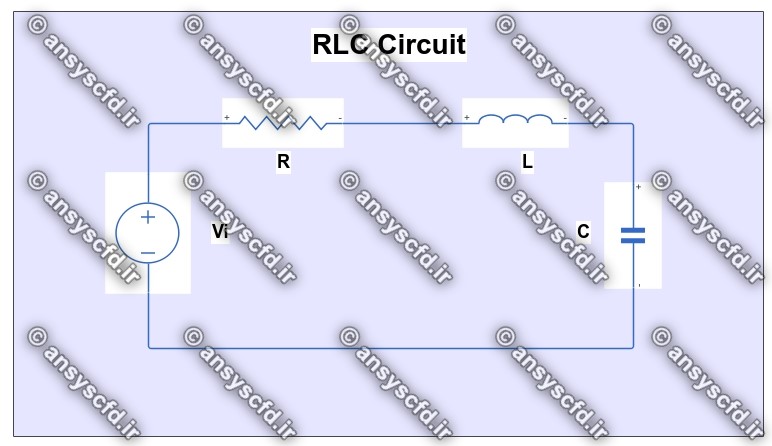
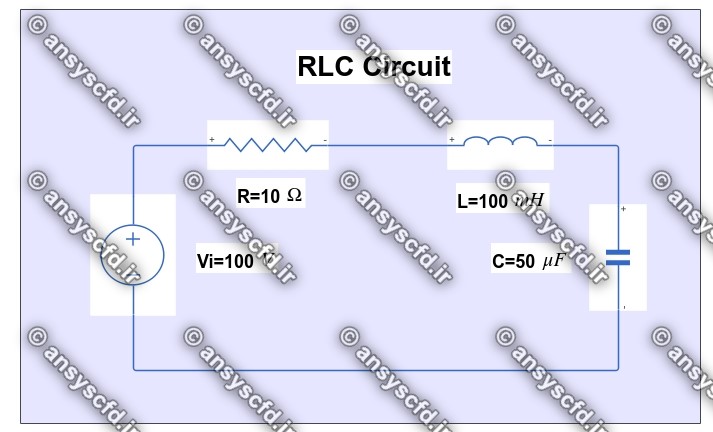
شکل مدار RLC سری
با نوشتن KVL برای مدار RLC سری مذکور می توان نوشت:
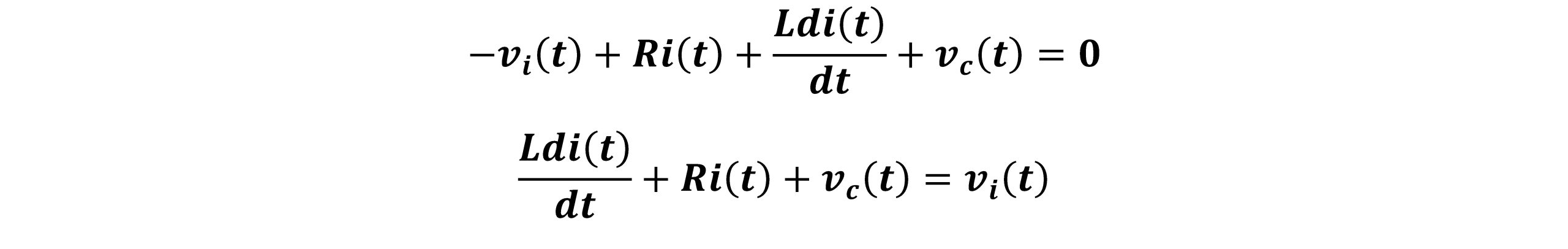
(1)
با تقسیم طرفین معادله به L داریم:
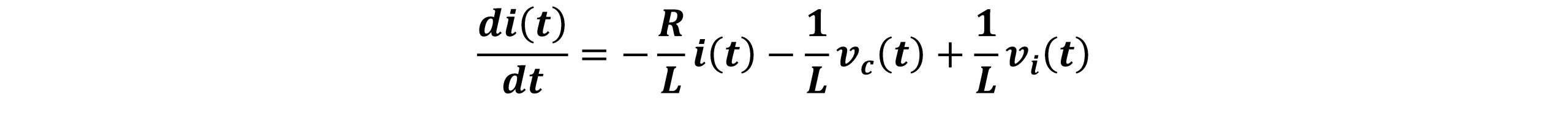
(2)
با نوشتن معادله جریان دو سر خازن داریم:
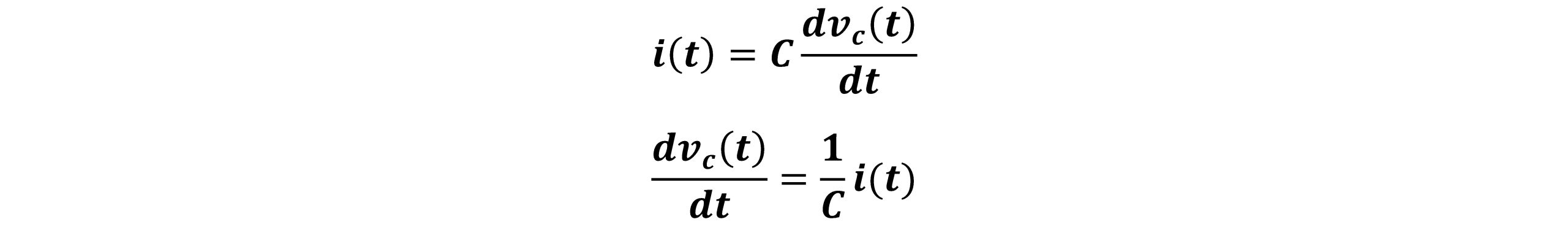
(3)
می توان معادلات (2) و (3) را به شکل کلی معادله فضای حالت بیان نمود:
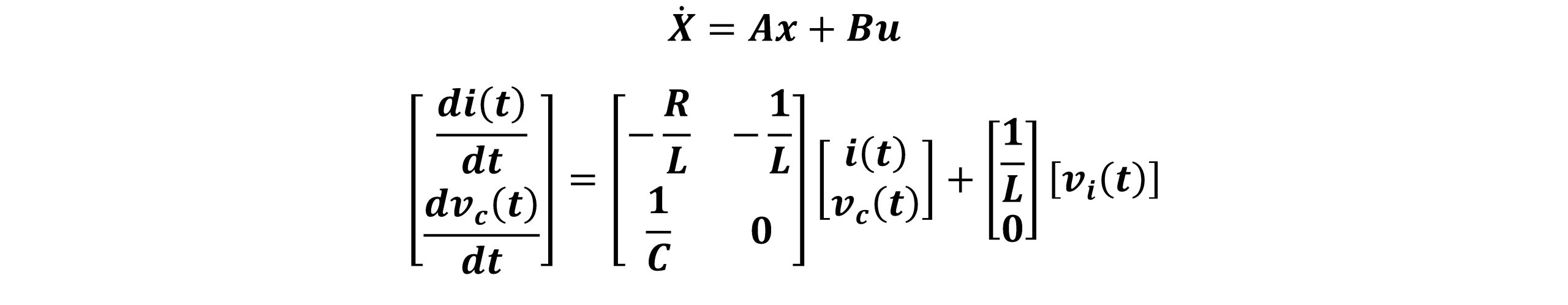
نمونه نتایج: