توضیحات

 

پروژه متلب پخش بار بهینه(OPF) با روش برنامه ریزی نیمه معین در سیستم توزیع

 

شبکه های قدرت از جمله پیچیده ترین سیستم های ساخته شده بدست انسان می باشند. این امر ناشی از وسعت جغرافیایی، تجهیزات متنوع بکاررفته در این سیستم ها و تعداد بالای قوانین و معادلات حاکم بر این سیستم ها است. درنتیجه مهندسان همواره نیازمند ابزارهای متنوع و قدرتمندی هستند، تا بواسطه آنها این سیستم ها را آنالیز و کنترل نمایند. از جمله این ابزارها میتوان به پخش بار، تخمین حالت، تولید خودکار و پخش بار بهینه اشاره نمود. پخش بار بهینه از جمله مواردی است که از روز معرفی آن توسط کارپنتیر در سال 1962 بسیارمورد بحث و مطالعه قرار گرفته است. هدف نهایی از پخش بار درواقع پیداکردن نقاط کار بهینه از دیدگاه های مختلف در یک سیستم قدرت می باشد، در حالی که معادلات پخش بار را مرتفع نموده و محدودیتهای مربوط به تمامی تجهیزات را در یک شبکه در نظرگیرد. برای این نقاط کار، متغیرهای کنترلی از جمله توان تولیدی ژنراتورها، ولتاژ ژنراتورها، محل قرارگیری تپ ترانسفورماتورها، بانک های خازنی و سلفی میتواند در نظر گرفته شود.

باتوجه به اینکه سیستم قدرت به علت افزایش دائمی تقاضا در بارهای صنعتی و خانگی دائما در حال گسترش و پیچیده شدن میباشد، ارائه ابزارهای مناسب برای کنترل، نظارت و تحلیل شبکه و یافتن تنظیمات بهینه برای کاهش هزینه ها، افزایش ایمنی انتقال و تولید نیروی الکتریکی و سود تولیدکنندگان توان با روشی دقیق و همزمان با تغییرات سریع سیستم و عرضه و تقاضا هر روزه نیازی ضروری تر میشود. از جمله مهمترین این ابزارها پخش بار بهینه در سیستم قدرت می باشد که وظیفه ارائه بهترین تنظیمات سیستم را با توجه به قیود ایمنی و محدودیت های تجهیزات را بر عهده دارد.

مسائل بهینه سازی در رشته های گوناگون علم و تکنولوژی وجود دارند. گاهی این مسائل میتوانند باتوجه به طبیعت مسئله، تابع هدف و قیود بسیار پیچیده شوند. در حل مسائل بهینه سازی با وجود اثبات کارآمدی، محکم بودن و پایه تکنیک های دیگر بودن روش های سنتی مانند برنامه ریزی خطی و غیرخطی، نقطه داخلی و نیوتن، این روش ها با مشکلاتی مانند ماندن در بهینه محلی، افزایش حجم محاسبات و قابل اجرانبودن برای مسائل خاص روبرو هستند. این مشکلات باعث به وجود آمدن تکنیک های بهینه سازی تکاملی و تصادفی شدند که به سرعت بر محدودیت های قبلی فائق می آیند.

مسئله پخش بار بهینه یکی از پیچیده ترین مسائل بهینه سازی مطرح شده در سیستم قدرت می باشد که تابحال تکنیک های مختلف ابداعی بر آن پیاده شده اند. هدف OPF تنظیم بهینه شبکه قدرت است که این هدف از طریق بهینه کردن توابع ویژه ای تحت قيود خاصی صورت می گیرد. از این قیود می توان معادلات پخش بار شبکه، محدودیت های امنیتی و محدوده عملکرد تجهیزات شبکه را نام برد.

متغیرهای کنترلی مختلف مانند توان حقیقی خروجی ژنراتورها، ولتاژ مرجع ژنراتورها، بانکهای خازنی و سلفی، تپ تپ چنجرها، شیفت دهنده های فاز، تغییر داده می شوند تا از این طریق یک نقطه کار بهینه بسته به فرمول بندی مسأله حاصل شود. مشکل اساسی در حل مسأله پخش بار بهینه، وجود همزمان متغیرهای پیوسته(توان حقیقی و ولتاژ خروجی ژنراتورها) و گسسته (تپ تپ چنجر ها، شیفت دهنده های فاز و ورود و خروج بانک های خازنی و سلفی) است، متداول ترین تابع هدفی که برای این مسأله انتخاب می شود کمینه کردن هزینه سوخت نیروگاه ها است.

از دیگر اهداف درنظرگرفته شده میتوان کمینه کردن تلفات شبکه انتقال، نزدیک کردن سطح ولتاژ باس ها به مقدار یک پریونیت، کاهش میزان آلودگی واحدها، کاهش تعداد اعمال کنترلی و حذف بارها را نام برد. فرآیند تجدید ساختار در صنعت برق اهداف دیگری همچون بالا بردن رفاه اجتماعی و سود تولیدکننده ها را به این اهداف افزوده است.

محققان برای فرمول بندی ریاضیOPF روش های حل بسیاری را ارائه داده اند که می توان آنها را به سه دسته کلی مسأله خطی با متغیرهای کنترل پیوسته، مسأله غیر خطی با متغیرهای کنترل پیوسته و ترکیب مسأله خطی و غیر خطی با هر دو نوع متغیر پیوسته و گسسته تقسیم نمود:

روشهای بسیار زیادی برای حل این مسأله ارائه شده است که برخی از مشهورترین آنها عبارتند از: برنامه ریزی خطی، برنامه ریزی متوالی درجه دو، گرادیان، روش نیوتون و نقطه داخلی. علیرغم اینکه بعضی از این روش ها مشخصه همگرایی خوبی دارند و بطور گسترده ای در صنعت مورد استفاده قرار می گیرند موانع و مشکلاتی نیز دارند:

1- این روش ها عموما کمینه محلی را پیدا می کنند، مخصوصا اگر حدس اولیه در نزدیکی یک کمینه محلی باشد. این مشکل از شرایط توقف ناشی می شود.

2- هر روش باید متناسب با نحوه فرمول بندی تابع هدف و قیود اصلاح شود.

3- هر کدام از این روش ها پیش فرض هایی در مورد طبیعت مسأله می کنند که ممکن است درست نباشد. از جمله این فرض ها می توان مشتق پذیری، محدب بودن و پیوستگی را نام برد.

به منظور غلبه بر چنین مشکلاتی روش های جدید بهینه سازی ارائه شدند. از جمله مشهورترین این روش ها میتوان الگوریتم ژنتیک، تکامل تفاضلی، برنامه ریزی تکاملی، شبکه های عصبی مصنوعی، شبیه ساز حرارتی، جستجوی باکتریایی و بهینه سازی دسته ذرات را نام برد.

یک برنامه پخش بار بهینه(OPF) باتوجه به محدودیت های امنیت سیستم قدرت، طرحی برای کنترل سیستم قدرت ارائه می کند که ضمن حداقل شدن هزینه های بهره برداری، سطح معینی از امنیت سیستم تأمین گردد. آنچه معمولاً دریک برنامه پخش بار بهینه مورد توجه قرار می گیرد، قابل قبول بودن پروفایل ولتاژ در شرایط کار عادی و شرایط بروز حادثه است که از آنها به عنوان محدودیت های استاتیکی امنیت یاد می شود. در عمل، آنچه برای شرکت های تأمین برق در شرایط کنونی مورد توجه است، حفظ پایداری ولتاژ و رعایت محدودیت هایی است که از آنها به محدودیت های دینامیکی امنیت سیستم یاد می شود.

پخش بار بهینه به طور گسترده ای در برنامه ریزی و بهره برداری از سیستم های قدرت مورد استفاده قرار میگیرد. هدف از یک برنامه پخش بار بهینه مرسوم، یافتن مطلوب ترین حالت بهره برداری از سیستم قدرت است که در آن، ضمن رعایت مجموعه ای از محدودیتها، هزینه های تولید و انتقال انرژی الکتریکی(شامل هزینه تلفات و تولید) حداقل شود. اما ممکن است نقطة کار بدست آمده از محاسبات OPF مرسوم، قیود لازم برای بهره برداری امن از سیستم از نظر ناپایداری ولتاژ را نقض نماید. به عبارت دیگر ممکن است با وجود عملکرد اقتصادی سیستم، در صورت افزایش بار و یا وقوع اغتشاشی، سیستم به سمت فروپاشی ولتاژ میل کند. به همین دلیل امروزه سعی می شود قید پایداری ولتاژ نیز در یک برنامه پخش بار بهینه منظور شود. به مسئله پخش بار بهینه ای که دارای یک قید اضافی مربوط به پایداری ولتاژ باشد، پخش بار بهینه مقید به پایداری ولتاژ  گفته می شود.

پخش بار بهینه(OPF)

یک سیستم قدرت نیازمند ابزارهای خاصی برای تحلیل، مانیتورکردن و کنترل دارد. بیشتر این ابزارها به گونه مناسبی به شکل مسائل بهینه سازی فرمول بندی شده اند. OPFیکی از این ابزارهای مهم است که از زمان معرفی آن در دهه میلادی۶۰ به طور گسترده ای مورد توجه بوده است.

مطالعات پخش بار رکن اساسی تجزیه و تحلیل در سیستم های قدرت محسوب می شود. یک مسئله پخش بار معمولی، درواقع به دنبال حل مجموعه ای از معادلات جبری غیرخطی حاکم بر سیستم قدرت است که بیانگر اجزاء سیستم تولید و انتقال انرژی الکتریکی هستند و مقدار و جهت جاری شدن توان حقیقی و راکتیو در سیستم و ولتاژ شینها را تعیین میکند. اما الگوریتم های یک برنامه پخش بار معمولی بطور خودکار درصدد حداقل ساختن هیچ تابع هدفی، نظیر هزینه تولیدیا تلفات انتقال نیست، بلکه صرفا یک پاسخ موجه را می یابد.

پخش بار بهینه درواقع یک فرآیند تکراری است که با استفاده از تکنیک های بهینه سازی ریاضی، درصدد یافتن مناسب ترین شرایط بهره برداری از سیستم است که ضمن رعایت همه محدودیت های بهره برداری، برخی معیارها که در تابع هدف مسئله تبلور یافته اند، بهینه نماید. داده های ورودی و خروجی یک مسئله پخش بار بهینه مشابه مسئله پخش بار عادی هستند. اما تابع هدف مسئله عموما به فرم تلفات توان اکتیو، میزان تولید توان راکتیو، هزینه تولید توان اکتیو توسط ژنراتورها و یا ترکیبی از آنها می باشد.

OPF در ابتدا به شکل دنباله طبیعی از پخش بار اقتصادی(ELD) فرمول بندی شد، هرچند تفاوت هایی بینOPF و ELD وجود دارد. در یک برنامه پخش بار اقتصادی کلاسیک، هدف تأمین بار مصرفی کل سیستم با صرف کمترین هزینه برای تولید انرژی الکتریکی است. در یک برنامة پخش بار اقتصادی کلاسیک، هیچ قید امنیتی در محاسبات منظور نمیشود. اما در پخش بار بهینه، هدف این است که طوری از سیستم بهره برداری شود که ضمن تأمین توان مورد نیاز بارها، تابع هدفی که در آن علاوه بر هزینه تولید انرژی الکتریکی، قیود دیگری مانند میزان انحراف مجاز ولتاژ شین ها، تلفات سیستم، قيود تجهیزات سیستم و قیود امنیتی درنظر گرفته شده است، مینیمم شود.

مسئله پخش بار بهینه در ابتدا در اوایل دهه میلادی۱۹۶۰ توسط Carpentier مطرح و سپس توسط Dominel و Tinney در سال ۱۹۶۸ به تفصیل معرفی گردید. در طی دهه ۸۰ و ۹۰ میلادی تحقیقات متعددی در زمینه پخش بار بهینه با توجه به محدودیت های استاتیکی امنیت سیستم صورت گرفت و روشهای متعددی نیز به تناسب ساختار مدل های پیشنهاد شده، مورد استفاده قرار گرفت که از آن جمله می توان به روش گرادیان (Sun و همکاران ۱۹۸۴ – Harsan و همکاران ۱۹۹۷)، روش نیوتن (Buchet و همکاران ۱۹۸۴ )، روش تجزیه P-Q (Shoult و همکاران، 1982)، روش نقطه درونی ( Momoh و همکاران ۱۹۹۴- Aguado و همکاران ۱۹۹۷)، روش فازی (Romesh و همکاران ۱۹۹۷) و الگوریتم های تکاملی مبتنی بر هوش محاسباتی، اشاره کرد.

متغيرها:

متغیرهایی که میتوان آنها را برای رسیدن به حل بهینه تنظیم نمود، متغیرهای کنترلی نامیده میشوند. این متغیرها شامل توان اکتیو تولیدی ژنراتورها به غیر از ژنراتور مبنا (مرجع)، دامنه ولتاژ شین های دارای ژنراتور، تپ ترانسفورماتورهای دارای تپ چنجر، تنظیمات شیفت دهنده های فاز، خازن ها و راکتورهای سوئیچ شونده، تنظیمات ادوات FACTSو … هستند. متغیرهای کنترلی میتوانند پیوسته، مانند دامنه ولتاژ و توان اکتیو تولیدی ژنراتورها و …. و یا گسسته مانند، تپ ترانسفورماتورها و منابع توان راکتیو و … باشند. متغیرهای گسسته را میتوان با پله های کوچک و با دقت مناسب وارد مسئله نمود.

متغیرهای وابسته، متغیرهایی می باشند که مقادیر آنها به متغیرهای کنترلی وابسته است. این متغیرها می توانند دارای هر مقداری، البته در بین محدوده تغییراتشان، که بوسیله الگوریتم بهینه سازی بدست می آید، باشند. متغیرهای وابسته شامل: توان راکتیو تولیدی در شین های دارای ژنراتور به غیر از شین مبنا، دامنه ولتاژ شینهای بار، توان اکتیو و راکتیو عبوری از خطوط انتقال و ترانسفورماتورها و … هستند.

توابع هدف:

هدف اصلی یک برنامه OPF، بدست آوردن(تنظیم) مقادیری برای متغیرهای کنترلی سیستم است که به ازای آنها، مقدار یک تابع هدف بهینه شود. توابع هدف انواع مختلفی دارند. انتخاب تابع هدف باید براساس تجزیه و تحلیل های دقیق بر روی امنیت، اقتصاد و شرایط کاری سیستم های قدرت صورت پذیرد. بعضی از پرکاربردترین توابع هدف عبارتند از: مینیمم کردن هزینه سوخت، تلفات سیستم، تعداد اعمال کنترلی، ظرفیت خطوط انتقال، مینیمم کردن هزینه سرمایه گذاری توان راکتیوو غيره. عموماً هزینه سوخت برای تولید توان توسط ژنراتورها از پرکاربردترین تابع هدف در مطالعات OPF می باشد.

در برخی از موارد، ترکیبی از توابع هدف بیان شده در بالا مورد استفاده قرار می گیرد که به آن پخش بار بهینه چندهدفه گفته می شود. به طور مثال، مینیمم کردن همزمان هزینه سوخت و تلفات سیستم یکی از توابع چندهدفه می باشد. در چنین حالتی یک ضریب وزنی برای تعیین میزان اهمیت هر یک از اعضای تابع هدف، مورد نیاز است.

قیود:

قيود موجود در پخش بار بهینه را میتوان به دو دسته کلی، قیود تساوی و قیود نامساوی تقسیم بندی نمود.

قیود تساوی:

قيود تساوی همان معادلات پخش بار هستند که برقراری آنها اجباری است. این قیود تعادل توان اکتیو و راکتیو را در شبکه تضمین میکنند. با استفاده از معادلات پخش بار، وسیله ای برای برقراری تعادل توان اکتیو و راکتیو که در حین بهره برداری در شرایط مانا در شبکه وجود دارد، فراهم می شود. زمانیکه یک حل قابل قبول برای پخش بار وجود داشته باشد، این قیود (تعادل توان اکتیو و راکتیو) برقرار می باشند، در غیر این صورت مسئله OPF غیر عملی است. معادلات پخش بار ارتباط بین متغیرهای کنترلی و متغیرهای وابسته را نشان میدهد.

قیود نامساوی:

تمامی متغیرها دارای حدود بالا و پایین هستند که باید در بدست آوردن حل بهینه، رعایت شوند. قیود بر روی متغیرهای کنترلی موجب می شود که در شرایط بهره برداری، حدود مربوط به تجهیزات سیستم، رعایت شود.

عمومأ حدود توان اکتیوو دامنه ولتاژ واحدهای تولیدی از مهم ترین این حدود هستند. قیود نامساوی به دو دسته زیر تقسیم بندی می شوند: الف) محدودیت های فیزیکی بر روی متغیرهای کنترلی، ب) محدودیت های بهره برداری در سیستم های قدرت. بسیاری از قیود دیگر مانند، قیدهای امنیت و انواع پایداری سیستم های قدرت نیز می توانند در این دسته قرار بگیرند و در این صورت می توان مسئله OPF را گسترش داد.

بهینه سازی:

در طی سالهای گذشته روشهای متعددی برای حل مسئله OPF بکارگرفته شده است. اساس همه این روشها را تکنیک های بهینه سازی تشکیل میدهد. OPF، شاید مهمترین تکنیک برای بدست آوردن کمترین هزینه تولید در یک سیستم قدرت با قيود خاص باشد.

مسئله بهینه سازی درواقع عبارت است از مینیمم کردن یک تابع هدف معین با متغیرهای مشخص، به طوریکه جواب بدست آمده در حوزه تعریف شده در مسئله باشد و همچنین قیود در نظر گرفته شده در مسئله نیز، برقرار باشد.

از بزرگترین موانع یک جستجوی بهینه موفق، یکی زمان محاسبات و دیگری عدم همگرایی به جواب بهینه عمومی (کلی) است. مینیمم محلی یک حل قابل قبول می باشد که تابع هدف را در محدوه خاصی مینیمم مینماید، ولی در مینیمم کلی کمترین مقدار تابع هدف در كل ناحیه قابل قبول، بدست می آید. در بسیاری از مسائل مانند بهینه سازی هزینة سوخت و ایجاد تعادل بار در شبکه های توزیع تجدید ساختاریافته، که از مسائل بسیار پیچیده و غیرخطی هستند، استفاده از روش های کلاسیک و غیر هوشمند برای بهینه سازی، دشوار و یا شاید ناکارا باشد. بهینه سازی میتواند به روشهای مختلفی انجام پذیرد، که می توان آنها را به صورت زیر طبقه بندی نمود:

روش های برنامه ریزی ریاضی:

انواع روشهای حسابی و ریاضی، برنامه ریزی خطی(LP)، برنامه ریزی غیرخطی(NLP)، برنامه ریزی دینامیکی (DP)، برنامه ریزی مرتبه دوم(QP)، روش نقطه درونی(IPM)، برنامه ریزی با اعداد صحیح، روش گرادیان مزدوج، روش بیشترین کاهش، برنامه ریزی با چند هدف، و نظریه بازی و … در این طبقه جای می گیرند. شایان ذکر است که به این دسته، روش های مرسوم و یا کلاسیک نیز گفته می شود.

روش های فرآیند تصادفی:

در این روش ها از قوانین احتمالات استفاده می شود و شامل فرآیند مارکوف، مونت کارلو و … می باشد.

روشهای آماری:

همان طور که از نام این روش ها پیدا است، اساس این روشها را فرآیندهای آماری مانند تحلیل رگرسیون، شناسایی الگوی آماری و … تشکیل میدهد.

روش های جستجوی اکتشافی:

این روش ها مبنای ریاضی چندانی ندارند و اساس آنها جستجو در فضای تصمیم­گیری بر مبنای یک سری قواعد تجربی بسته به ماهیت مسئله بهینه سازی در مورد رد یا انتخاب متغيرها، مسیر جستجو و اصول تجربی برای محدودکردن فضای جستجو میباشد و همان گونه که از نام آنها بر می آید، به صورت ذهنی و اکتشافی می باشند.

روشهای جستجوی هوشمند:

از ویژگی های این دسته، میتوان به تطبیقی بودن مسیر جستجو، مقاوم بودن، نامعین بودن قواعد و عدم نیاز به مدل سازی دقیق سیستم و همچنین توانایی تعمیم این روشها، اشاره کرد. شبیه سازی تبرید(SA)، جستجوی ممنوع(TS) برنامه ریزی تکاملی(EP)، الگوریتم تکامل تفاضلی(DE)، الگوریتم ژنتیک(GA)، بهینه سازی گروه ذرات(PSO)، الگوریتم بهینه سازی مورچگان(ACO)، تئوری مجموعه فازی(FST) و شبکه عصبی مصنوعی(ANN) و … را میتوان جزء این دسته محسوب نمود. به این دسته از بهینه سازی، روش های بهینه سازی مدرن نیز گفته می شو.

در حالت کلی مسئله OPFیک مسئله بهینه سازی غیرخطی، غیر محدب و استاتیک است که در آن متغیرهای کنترلی میتوانند از هر دو نوع پیوسته(مانند توان و ولتاژ ژنراتورها) و گسسته (مانند تپ ترانسفورماتورها و خازن های شنت) باشند، که البته این گسسته بودن، به پیچیدگی حل مسئله می افزاید.

بیشتر روش هایی که در گذشته برای حل مسئله OPF مورد استفاده قرارگرفته اند، بر مبنای بهینه سازی به روش برنامه ریزی ریاضی(روش کلاسیک) بوده اند. در چهار دسته اول از روشهای بهینه سازی، اگرچه برخی از آنها دارای مشخصه همگرایی بسیار خوبی هستند و برخی دیگر نیز به طور وسیعی در صنعت مورد استفاده قرار گرفته اند، اما دارای نقاط ضعفی به شرح زیر می باشند: 1- همگرایی به نقطه بهینه سراسری(کلی) یا محلی، وابستگی شدیدی به شرایط اولیه دارد. بدین معنی که اگر شرایط اولیه در مجاورت نقطه بهینه محلی انتخاب شود، پاسخ بدست آمده به جای آنکه بهینه سراسری باشد، تنها یک بهینه محلی خواهد بود.

۲- انتخاب هر کدام از روشهای این چهار دسته براساس ماهیت ریاضی توابع هدف و قیود آنها صورت می پذیرد.

3-روشهای کلاسیک بر پایه برخی فرض های تئوری از قبیل همواری، مشتق پذیری و پیوستگی که ممکن است برای شرایط واقعی مناسب نباشند، بسط داده شده اند.

۴- در این روشها راه حل مناسبی برای بدست آوردن پاسخ بهینه، در توابعی که شامل متغیرهای گسسته هستند، در نظر گرفته نشده است.

اما مهمترین ضعف این روش ها، ناتوانی در پیدانمودن نقطه بهینة کلی میباشد. برای غلبه بر ضعفهای فوق، استفاده از روش های جستجوی هوشمند(روش های مدرن) سرعت گرفته است. البته این روشهای جدید نیز زمان زیادی برای انجام محاسبات نیاز دارند که باتوجه به پیشرفتهای صورت گرفته در تکنولوژی رایانه و استفاده از پردازش موازی، این مشکل قابل حل است.

پخش بار بهینه مقید به پایداری ولتاژ:

پخش بار بهینه مقید به پایداری ولتاژ در مقایسه با پخش بار بهینه دارای یک قید اضافی است. این قید، پایداری ولتاژ سیستم را حتی پس از وقوع یک یا چند خطای معین، تضمین می نماید. باید توجه داشت که در یک سیستم قدرت تعداد بی شماری از انواع خطا قابل تعریف است؛ ولی در طراحی یک سیستم قدرت خاص باتوجه به عملکرد گذشته آن، خطاهای خاصی که به آن خطاهای محتمل گفته میشود در نظر گرفته می شوند.

مسأله بهینه سازی به طور گسترده ای در حل بسیاری از مسائل در حوزه های علمی و صنعتی مطرح میشود. در بعضی موارد این مسائل به دلیل ماهیت عملی و کاربردی تابع هدف و یا محدودیت های مدل موجود، میتوانند بسیار پیچیده باشند. به طور مرسوم روش های بهینه سازی بر پایه مشتق گیری بنا شده اند. این روش های بهینه سازی کارایی خود را در بسیاری از مسائل بهینه سازی نشان داده اند، ولی میتوانند با مشکلاتی از قبیل گرفتار شدن در مینیمم محلی، افزایش پیچیدگی محاسبات، زمان بر بودن و قابل استفاده نبودن برای برخی از توابع هدف، مواجه شوند. طبیعت، الهام بخش محققان برای توسعه مدل هایی برای حل مسائل بوده است. بهینه سازی زمینه ای است که به کرات توسط این مدل های طبیعی توسعه داده شده و به کاررفته است.

دو گروه مهم از الگوریتم های بهینه سازی در این زمینه، الگوریتم های تکاملی و الگوریتم های مبتنی بر هوش جمعی(SI) هستند. هوش جمعی، عوامل یا دسته هایی که باهم همکاری میکنند و توانایی خود سازماندهی و تقسیم کار دارند را مدل سازی مینماید. جمعیت مورچه ها، دسته پرندگان، دسته ماهی ها، سیستم ایمنی بدن و جمعیت زنبورهای عسل، مثال هایی از یک سیستم جمعی هستند. الگوریتم بهینه سازی جمعیت مورچگان (ACO)، رفتار کاوشی مورچه ها را شبیه سازی می کند. الگوریتم بهینه سازی گروه ذرات (PSO)، زندگی جمعی دسته های پرندگان با دسته های ماهی ها را مدل سازی می کند. الگوریتم سیستم ایمنی مصنوعی (AIS)، در واقع شبیه سازی توده های سلولی سیستم حفاظتی میباشد.

الگوریتم بهینه سازی گروه ذرات(PSO)، یک روش جستجوی ابتکاری نسبتا جدید است که مکانیزم آن از رفتارهای گروهی جمعیت های زیستی الهام گرفته شده است. از زمان ارائه این الگوریتم در سال ۱۹۹۵ در  محققان بسیاری در زمینه های مختلف علوم به بررسی قابلیت های این روش پرداخته و در برخی موارد حتی اصول اولیه این الگوریتم را تغییر داده اند. PSO مانند الگوریتم ژنتیک (GA)، یک الگوریتم تکاملی بر مبنای جستجوی جمعیت است که در تطبیق و طراحی کنترلرها و کاربردهای دیگر، محبوبیت قابل توجهی پیدا کرده است. درواقع PSO و GA از یک مجموعه از نقاط(جمعیت)، به مجموعه دیگری از نقاط در یک تکرار واحد حرکت می کنند و در طی این حرکت، به طور محتمل و با استفاده از ترکیب قوانین احتمالی و قطعی، بهبودهایی در پاسخ حاصل می شود.

 

GA و بسیاری از نسخه های آن در محیط های آکادمیک و صنعتی اساسأ به علت هوش بالا، سهولت اجرا و توانایی مؤثر در حل مسائل غیر خطی درجه بالا و بهینه سازی اعداد صحیح ترکیب شده که نوعی از سیستم های مهندسی پیچیده است، محبوبیت دارند. اما GA یک عیب اساسی دارد و آن هزینه محاسباتی بالای آن است. تحقیقات نشان داده است که PSO در برابر GA با همان کارایی (یافتن راه حل های بهینه سراسری یکسان)، هزینه محاسباتی کمتری دارد و به همین دلیل استفاده از آن در تحلیل ها در سال های اخیر با استقبال بالایی مواجه شده است.

هوش جمعی:

هوش جمعی(SI) براساس رفتار اجتماعی سیستم های خود سازمانده و نامتمرکز مطرح شده است. این بیان اولین بار به وسیلهGerardo Beni و Jing Wang در سال ۱۹۸۹ در زمینه رباتیک سلولی مطرح شد. سیستم های هوش جمعی معمولاً از جمعیتی از نمایندگان ساده که به طور محلی با یکدیگر و با محیط اطرافشان، اثر متقابل دارند تشکیل میشود. همچنین این نماینده ها از قوانین ساده ای پیروی می کنند. هرچند ساختار کنترلی متمرکزی بین نماینده ها وجود ندارد که مشخص نماید هر نماینده شخصی چگونه باید رفتار کنند. اثر متقابل محلی میان نماینده ها به رفتار سراسری پیچیدهای منجر می شود.

در واقع هوش جمعی مثال ساده ای از رفتار جمعی است که در آن افراد برای رسیدن به یک هدف نهایی، با هم همکاری می کنند. این روش مؤثرتر از زمانی است که افراد جداگانه عمل می نمایند. گروه را می توان به صورت مجموعه های سازمان یافته از موجوداتی تعریف کرد که با یکدیگر همکاری می کنند. در طبیعت موجوداتی مانند مورچه ها، زنبور ها، موریانه ها، دسته های ماهیان و دسته های پرندگان دارای هوش جمعی هستند. در این نوع اجتماعات هر یک از موجودات ساختار نسبتا ساده ای دارند ولی رفتار جمعی آنها بی نهایت پیچیده است. برای مثال در کولونی مورچه ها، هر یک از مورچه ها یک کار ساده ی مخصوص به خود را انجام می دهد ولی به طور جمعی، عمل و رفتار مورچه ها، ساختن بهینهی لایهی محافظت از ملکه و نوزادان، تمیز کردن لانه، یافتن بهترین منابع غذایی و بهینه سازی استراتژی حمله را تضمین می نماید. رفتار کلییک گروه به صورت غیر خطی از ترکیب رفتارهای هریک از اعضای اجتماع بدست می آید؛ به عبارت دیگر، یک رابطه بسیار پیچیده بین رفتار جمعی و رفتار فردییک اجتماع وجود دارد. رفتار جمعی فقط وابسته به رفتار فردی افراد اجتماع نیست بلکه به چگونگی همکاری بین افراد نیز وابسته است. همکاری بین افراد، تجربه ی افراد دربارهی محیط شان را افزایش می دهد و موجب پیشرفت اجتماع می شود. ساختار اجتماعی گروه بین افراد مجموعه کانال های ارتباطی ایجاد می کند که طی آن افراد می توانند به تبادل تجربه هایشخصی خود بپردازند.

الگوریتم بهینه سازی گروه ذرات (PSO)

الگوریتمPSOیک الگوریتم جستجوی اجتماعی است که از روی رفتار اجتماعی دسته های پرندگان مدل شده است. در ابتدا این الگوریتم به منظور کشف الگوهای حاکم بر پرواز همزمان پرندگان و تغییر ناگهانی مسیر آنها و تغییر شکل بهینهى دسته، به کار گرفته شد. در حقیقتPSOیک تکنیک بهینه سازی تصادفی قوی بر اساس حرکت و هوش گروه ها می باشد که از رفتار دسته جمعی دسته ای از پرندگان یا گروهی از ماهی ها الهام گرفته است. این الگوریتم مفهوم اثر متقابل اجتماعی را برای حل کردن مسئله به کار می برد و در سال ۱۹۹۵ توسط James Kennedy (روان شناس اجتماعی) و Russell Ebrehart (مهندس الکترونیک) توسعه یافت. این الگوریتم با تکنیک های محاسباتی تکاملی دیگر مانند الگوریتم ژنتیک شباهت هایی دارد. با هر ذره، به عنوان یک نقطه در فضایN بعدی رفتار میشود که پروازش را برطبق تجربیات پرواز خود و همچنین تجربیات پرواز دیگر ذره ها، تنظیم میکند.

شکل رفتار دسته جمعی گروهی از ماهیان و پرندگان.

 

در الگوریتمPSO هر ذره مسیرش را در مختصات فضای حل ادامه می دهد که مرتبط با بهترین حلی میباشد که تاکنون به وسیله آن ذره بدست آمده است. این مقدار بهترین پاسخ شخصی (pbest) نامیده می شود. بهترین مقدار دیگر که PSO آن را دنبال میکند، بهترین پاسخی است که تاکنون به وسیله تمام ذره ها که در همسایگی هم هستند، بدست آمده است. این مقدار بهترین پاسخ کلی (gbest) نامیده می شود.

ایده اصلی در PSO، شتاب گرفتن هر ذره نسبت به مکان هایpbest خود و gbest، با در نظر گرفتن یک شتاب دهنده وزن داده شده به طور تصادفی، در هر مرحله زمانی است.

PSO رفتار گروهی از پرندگان را شبیه سازی می کند. سناریو زیر را در نظر بگیرید: یک گروه از پرندگان به طور تصادفی در حال جستجوی غذا در یک ناحیه می باشند و تنها یک قطعه غذا در ناحیه مورد جستجو قرار دارد. هیچیک از پرندگان اطلاعی از مکان غذا ندارند اما می دانند که در هر مرحله چه فاصله ای از غذا دارند. بنابراین مسئله در اینجا یافتن بهترین راه حل برای پیدا کردن غذا می باشد. یک روش مؤثر دنبال کردن پرندگانی می باشد که نزدیکترین فاصله را به غذا دارند. PSO از این سناریو یادگیری کرده و از آن برای حل مسائل بهینه استفاده می کند. در PSO هر حل واحد، معادل با یک پرنده در فضای جستجو می باشد ذره نام دارد. همه ذره ها دارای: 1) مقادیر مشخصی هستند که به وسیله تابع برازندگی که باید بهینه شود، ارزیابی میشوند ۲) دارای سرعت هایی در جهت پرواز دره های دیگر هستند، که در فضای مسئله به دنبال بهینه کنونی می باشند.

PSO با یک گروه از ذره های تصادفی آغاز میشود و سپس به جستجوی پاسخ بهینه با تولید پاسخهای اصلاح شده، اقدام میکند. در هر مرحله هر ذره باتوجه به دو مقدار بهینه اصلاح میشود. اولین مقدار بهینه، بهترین حلی است که تاکنون توسط آن ذره بدست آمده است(یعنیpbest) و دیگری بهترین مقدار سراسری می باشد که با gbest نشان داده شد. هنگامی که یک ذره بخشی از جمعیت را به عنوان همسایگی های مکانی در نظر می گیرد، بهترین مقدار به بهترین مقدار محلی تبدیل و lbest نامیده می شود. بعد از یافتن این دو مقدار بهترین، ذره سرعت و مکاتش را اصلاح می کند. هر ذره سعی می کند تا مکانش را با استفاده از اطلاعات زیر اصلاح کند: مکان های کنونی، سرعت های کنونی، فاصله میان مکان کنونی و pbest، فاصله میان مکان کنونی و gbest.

شکل فلوچارت کلی الگوریتمPSO.

در یک شبکه قدرت، مسئله پخش بار بهینه(OPF) یکی از مسائل بسیار مهم در مهندسی قدرت می‌باشد که به تعیین بهترین سطوح عملکردی نیروگاه‌های برق به منظور برآورده کردن تقاضای مورد نیاز در سراسر یک شبکه انتقال می‌پردازد. با توجه به معادلات غیرخطی/غیرمحدب مسئله پخش بار بهینه، روش‌های متعددی برای حل این مسئله از زمان طرح آن پیشنهاد شده‌اند. اخیراً روش‌هایی مبتنی بر محدب‌سازی برای مقابله با مشکل غیرمحدب بودن این مسئله ارایه شده‌‌اند که در مقایسه با سایر روش‌ها قادر به یافتن نقطه بهینه مطلق در بیشتر مسائل هستند. هرچند این روش‌ها نیز به نوبه خود دارای معایبی هستند ولی از آنجا که هزینه به دست آمده برای حل بهینه محلی می‌تواند بسیار بزرگتر از هزینه حاصل از بهینه مطلق باشد لذا نیاز به روش‌هایی که بتوانند جواب بهینه مطلق مسئله پخش بار بهینه را به دست آورند همواره احساس می‌شود.

در این پروژه روش برنامه ریزی نیمه معین(SDP) برای حل مسئله پخش بار بهینه(OPF) در شبکه های توزیع انجام شده است.

این تکنیک:

• از مولفه های متقارن برای کاهش کوپلینگ بین فازها در شبکه توزیع استفاده می کند.
• رگولاتورهای ولتاژ تب چنجر را برای درنظرگرفتن اثر آنها بر پروفیل ولتاژ مدلسازی می کند.
• به صورت تکراری بارها را برای نشان دادن وابستگی شان به ولتاژ بروزرسانی می کند.
• قیود ولتاژ را به دقت مدیریت می کند.

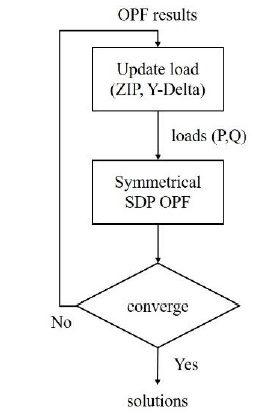
فلوچارت روش در شکل زیر نشان داده شده است.

 

شبیه سازی در نرم افزار متلب برای تست فیدرهای 123 گره انجام شده است.