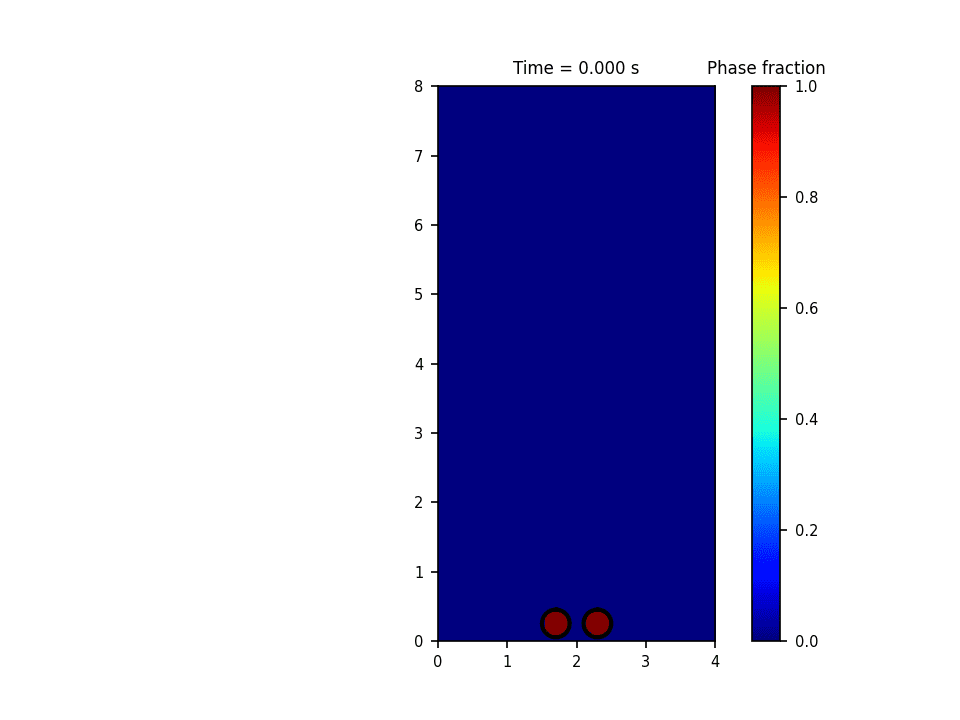
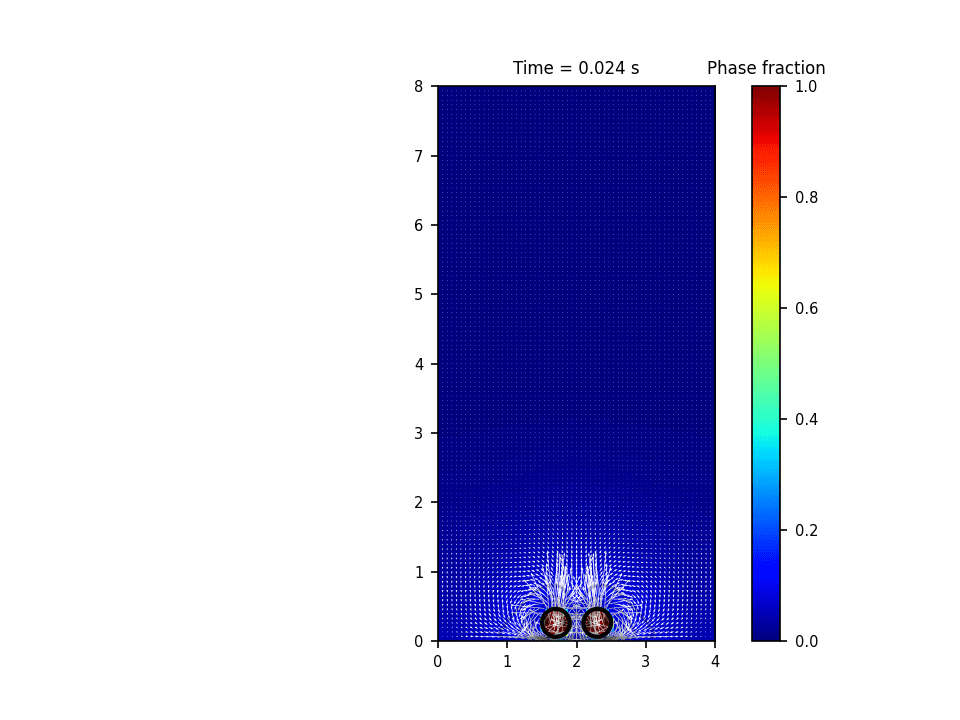
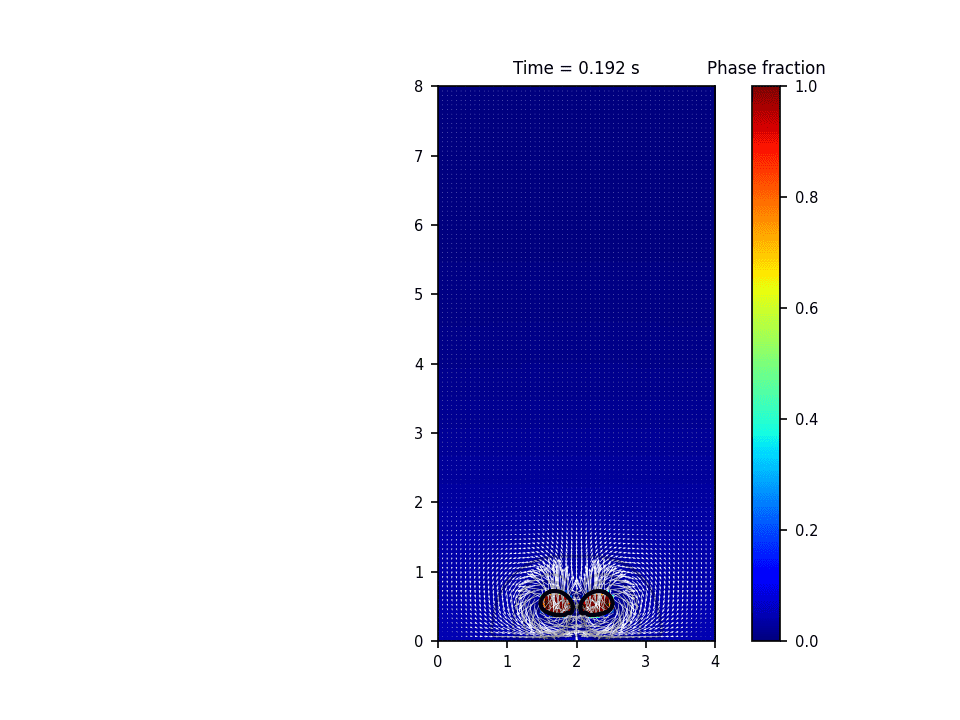
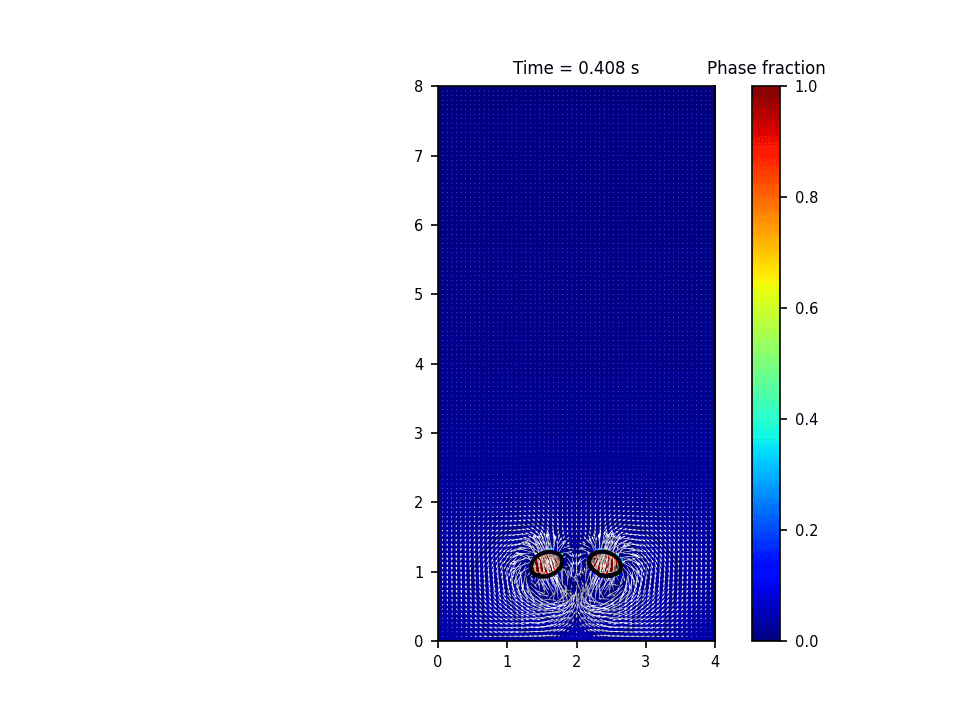
توضیحات

پروژه پایتون شبیه سازی فرآیند تشکیل و صعود حباب گاز در یک کانال عمودی به روش ردیابی یا پیشروی جبهه

دانلود مقاله مرجع

 

دانش پدیده های بین سطحی یکی از مباحث اصلی فیزیک می باشد که علاوه بر کاربردهای بسیار در صنایع مختلف، بسیاری از پدیده های طبیعی را توجیه می نماید. به عنوان نمونه بررسی ایجاد کف و ضدکف در مایعات، بررسی رفتار حباب ها، بررسی لایه های نازک، بررسی فصل مشترک مایعات امتزاج ناپذیر، بررسی کشش سطحی و کشش بين سطحی، ترشوندگی سطوح توسط مایعات و … جزئی از آن محسوب می شود. پدیده ها و خواص بین سطحی بر پایه نیروهای کوتاه برد بین مولکولی توضیح داده می شوند. نیروهای کوتاه برد بین مولکولی، همان نیروهایی هستند که عامل تغییر فاز یک ماده از حالت مایع به گاز می باشند. شناخت دینامیک و شیمی فیزیک پدیده های سطح، در صنایع مختلف، علوم پایه و پدیده های طبیعی پیرامون از اهمیت فراوانی برخوردار است. شناخت و پیش بینی پروسه تشکیل و صعود حباب و پدیده های انتقال مرتبط با آن از جمله نیازمندی های اساسی طراحی و کنترل فرآیندهای چندفازی است. به همین دلیل این مسئله مورد توجه بسیاری از محقق بوده و در چند دهه اخیر روش های آزمایشگاهی و تئوری های بسیاری در این رابطه مورد بررسی قرارگرفته است.

صعود حباب:

ماهیت یک حباب از سرعت صعود حباب، شکل و رفتار حرکتی آن تعیین می گردد. این سه مشخصه به خواص فیزیکی سیستم مخصوصا ویسکوزیته فاز مایع، جریان و خواص لایه حباب(بسته به حضور مواد فعال کننده سطحی) بستگی دارند. سرعت صعود مهمترین پارامتر در تشریح هیدرودینامیک و پدیده های انتقال در رآکتورهای حباب کار می باشد. بنابراین سرعت صعود حباب به عنوان نقطه ی شروع برای بررسی در چنین سیستم هایی قرار می گیرد. اندازه حباب، پارامتر متغیر مهمی برای تعیین سرعت صعود حباب و شكل حباب می باشد.

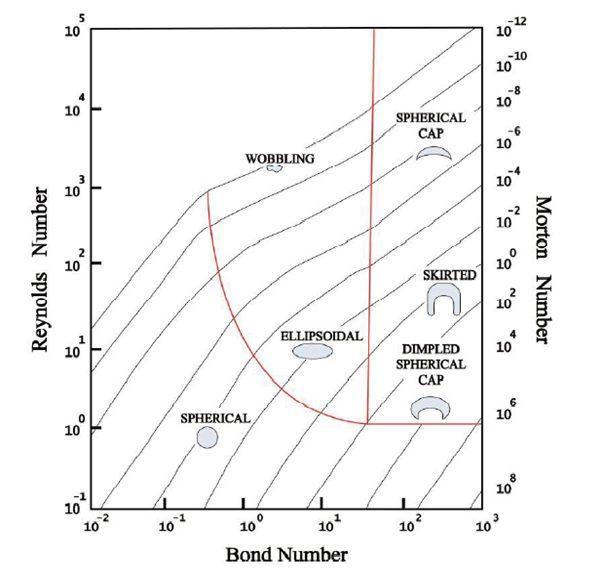
شکل تقسیم بندی حباب ها بر اساس شکل و اندازه.

 

همان طور که در شکل بالا دیده می شود حباب ها به سه دسته تقسیم می شوند:

-حباب های کروی

-حباب های بیضوی

-حباب های نیمه کروی.

حباب های بیضوی:

این دسته از حباب ها اشکال مختلفی دارند. ابعاد آنها به طور میانگین، بیضوی درنظرگرفته می شود. برخی از این حباب ها تخم مرغی شکل و دارای سطح محدب می باشند و برخی نیز اختلاف قابل ملاحظه ای با شکل بیضوی دارند. حرکت مارپیچ این حباب ها، یکی از عوامل تغییر شکل آنها می باشد. پیچیدگی حرکت حباب های بیضوی در مقاطع میانی بیشتر مشهود است.

حباب های کروی:

درصد کمی از حباب های صعود کننده در راکتورهای حباب کار تقریباً کروی می باشند. کروی بودن این حباب ها به دلیل غلبه نیروهای ویسکوز وارد بر جداره حباب بر نیروی اینرسی است که موجب چرخش حباب ها نیز می شود. سرعت نهایی این حباب ها توسط رابطه استوکس مشخص می گردد.

حباب های نیمه کروی:

شکل این گونه حباب ها بسیار شبیه یک نیم کره است و بیشتر تمایل به مسطح شدن دارند.

رژیم های شکل حباب:

رژیم کروی:

کشش سطحی و ویسکوزیته بر این رژیم حاکم می باشند. اندازة اصلی این حباب ها کوچک بوده و شکل حباب در هنگام صعود کروی یا تقریباً کروی باقی می ماند. معمولاً تغيير شكل محور اصلی (در راستای محور صعود) نسبت به محور فرعی کمتر از ۱۰ درصد هست.

رژیم بیضوی:

کشش سطحی عمدتاً بر این رژیم حاکم هست. اندازه این حباب متوسط و قطر و عدد باند آن به ترتیب معمولا در بازه 1.3 میلیمتر تا 6.0 میلیمتر و محدوده عدد باند از 0.25 تا 40 است. سرعت نهایی در یک سیستم خالص تقریبا با رابطه ای که توسط مندلسون بر پایه تئوری موج ارائه شد برابری می کند:

رژیم کلاه کروی:

نیروی اینرسی بر این رژیم حاکم است. اندازه حباب بزرگ و معمولا قطر آن از 6.0 میلیمتر بیشتر و نیز در  این الگو عدد باند از ۴۰ و عدد رینولدز از 1.2 بزرگتر است. سرعت نهایی حباب متناسب با اندازه حباب است. به علاوه به خاطر اینرسی بزرگ و وجود اختلاف فشار میان سطوح بالا و پایین، تغییر شکل های بزرگی در حباب هنگام صعود رخ می دهد. سرعت نهایی حباب به وسیله تئوری پیشنهادی توسط داویس و تیلور طبق تعریف زیر به دست می آید:

 

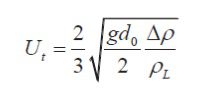
حرکت حباب:

حباب ها در اندازه های مختلف در صنایع تشکیل می شوند. اندازه این حباب ها تأثیر بسیار زیادی بر تغییر شکل این حباب ها دارد. هرچه اندازه حباب کوچکتر باشد به علت آن که انحنای سطح حباب بیشتر می شود، در نتیجه مقدار کشش سطحی آن بیشتر می گردد. حباب هایی که دارای کشش سطحی زیادی بر روی سطح خود هستند، در مقابل تغییر شکل از خود مقاومت نشان می دهند. هرچه حباب دارای مقدار شعاع بیشتری باشد به علت کشش سطحی کمتر دچار تغییر شکل بیشتر می گردد. این تغییر شکل ها می تواند موجب ایجاد شکل های بیضوی برای حباب و یا حتی پارگی شود.

در حرکت حباب در داخل سيال به سمت بالا، در صورتی که حباب از دیوار دور باشد حرکت در اثر نیروی شناوری آغاز می گردد. به علت حرکت حباب در سیال، به حباب نیروی پسا وارد می شود و در صورتی که حباب پاره نشود به یک سرعت و شکل ثابت خواهد رسید. در این سرعت نیروی شناوری با نیروی پسا برابری می کند و حباب با همین سرعت ثابت به حرکت خود ادامه خواهد داد. تغییر شکل حباب معمولا به شکل فرورفتگی از ناحیه پایین سطح محدب است. علت آن این امر است که در اثر اختلاف فشار بین سطح پایین و بالایی حباب نیرویی از مرز پایین حباب به سمت بالا وارد می گردد. در صورتی که مقدار کشش سطحی نتواند موجب تغییر شکل حباب گردد، فرورفتگی در وسط حباب که بیشترین اختلاف فشار را با سطح بالایی دارد، ایجاد میشود. در اثر این انحنای شدید مقدار کشش سطحی به شدت افزایش می یابد و ممکن است بتواند بر اختلاف فشار غلبه کند، در غیر این صورت این رشد انحنا، افزایش یافته تا در نهایت برابر اختلاف فشار گردیده یا حباب پاره شود.

دینامیک سیالات محاسباتی(CFD):

در مکانیک سیالات تحلیلی معادلات کلاسیک تنها برای حالات محدودی از جریان ها (حدود ۸۰ مورد) به صورت تحلیلی قابل حل هستند. اگرچه این حل ها در درک دینامیک سیالات بسیار مفید هستند، ولی به ندرت برای تحلیل و طراحی مهندسی به کار می روند. از این رو مکانیک سیالات آزمایشگاهی برای درک پدیده های مختلف جریان مورد توجه بوده است، اما برای رسیدن به این اهداف نیاز به آزمایشگاه های مجهز می باشد و گاهی لازم است آزمایش های زیادی انجام شوند که نیاز به صرف وقت و هزینه ی زیادی دارند. نتایج در قالب گروه های بدون بعد و روابط نیمه تجربی ارائه می شوند و معمولا برای استفادهی صنعتی از نتایج آزمایش ها به افزایش مقیاس نیاز می باشد. اگر چه نظریه های اصلی برای حل عددی معادلات دیفرانسیل جزئی از بیش از یک قرن پیش ارائه شده اند، اما تا قبل از ورود کامپیوترهای دیجیتال عملا استفاده اندکی از آنها شده بود. تحول عظیم در قدرت ذخیره سازی و پردازش اطلاعات توسط کامپیوترها، باعث پیشرفت در روش های عددی حل معادلات دینامیک سیالات گردید. این امر باعث تولد یک شاخه تخصصی به نام دینامیک سیالات محاسباتی (CFD) گردید. CFD نیاز به فرضیات محدود کننده کمی دارد و تمام متغیرهای میدان جریان را به طور کامل توصیف می کند. روش های مربوطه به راحتی قابل استفاده هستند، و تعداد زیادی از فرآیندهای مربوط به جریان سیال را می توان به طور همزمان مطالعه کرد بنابراین مسائل کاملا پیچیده را می توان با CFD بررسی کرد. می توان شبیه سازی های CFD را پلی بین تئوری و واقعیت به حساب آورد.

شبیه سازی با CFD دارای این مزیت بزرگ است که می توان اطلاعات ارزشمندی دربارهی رفتار جریان را بدون انجام آزمایش به دست آورد، در این شبیه سازی ها این امکان فراهم می شود که بتوان عوامل مختلف موثر بر جریان را در مدل حذف و یا اضافه نمود و به این ترتیب سهم نسبی هرکدام از فرآیندهای جریان مشخص می شود درحالیکه فهم آنها از طریق آزمایش اگر غیرممکن نباشد، بسیار سخت است. به منظور دستیابی به یک شبیه سازی عددی مطلوب به کمک CFD باید معادلات و مدل های مناسب حاکم بر مساله را به دقت مورد ارزیابی و مطالعه قرار داده و مناسب ترین آنها را برای شبیه سازی سیستم انتخاب کرد.  در زیر انواع معادلات حاکم بر سیستم های چندفازی مورد بررسی قرار گرفته و سپس مدل مناسب برای شبیه­ سازی مساله حاضر انتخاب می شود.

جریان های چندفازی:

جریان های چندفازی عبارتند از جریان ذرات جامد در مایعات یا گازها، جریان قطرات در گازها، جریان حباب ها در مایعات یا ترکیبی از این موارد. در یک جریان چند فازی یک یا تعداد زیادی ذره که می تواند حباب، قطره و یا ذره جامد باشند، فاز دوم نامیده می شود. این فاز در داخل یک محیط در برگیرنده که فاز اول نامیده می شود، جریان دارد.

دینامیک جریان دوفازی از پدیده های بسیار پیچیده است، زیرا علاوه بر پیچیدگی جریان تک فازی، مشکلاتی در مکان های مرزی سطح مشترک، مومنتم بین فازی، انتقال حرارت، جرم و واکنش های درون فازی دارد. بسیاری از پدیده های روزمره در زندگی به نوعی از دیدگاه عملی، مسائل دوفازی یا چند فازی محسوب می شوند.

بررسی حرکت حباب در سیالات کاربردهای فراوانی در صنایع نفتی و شیمیایی دارد و علت آن مخلوط شدن گاز و مایع به طور وسیع در این صنایع است.

بررسی فرآیند تشکیل حباب در آزمایشگاه:

اغلب در بررسی فرآیند تشکیل حباب، از دستگاه هایی مشابه شكل زیر استفاده می شود. دستگاه بطورکلی شامل یک محفظه – مایع گاز و ستون مایع می باشد که در قسمت انتهایی ستون، اریفیس قرارگرفته است.

شكل دستگاه آزمایشگاهي.

معمولاً فرایند تشکیل حباب را تحت سه شرط مورد برسی قرار می دهند:

جریان – ثابت فشار ثابت و حالت متوسط.

فرض کنید گازی با دبی q_i وارد محفظه گاز گردد. فشار داخل محفظه با ورود گاز افزایش می یابد. در این حالت سطح مشترک گاز مایع در سر اریفیس، مسطح است و هیچ حبابی دیده نمی شود. در واقع یک برآمدگی با افزایش فشار داخل محفظه ایجاد می گردد تا اینکه فشار داخل محفظه به ماکزیم مقدار خود برسد. این فشار P_max از فشار هیدرو استاتیک مایع بالای نازل P_h بیشتر است. بنابراین ناگهان بر فشار هیدرواستاتیک غلبه کرده و حباب ایجاد می شود. این مرحله به عنوان قدم کاهش فشار یا جریان گاز خود به خودی نامیده می شود.

کاربرد و مثال هایی از جریان چندفازی:

بیشترین مسائل در مهندسی نیز از جریان های دوفازی نشأت می گیرد، زیرا این جریان در کاربردهای صنعتی متفاوت از جمله فیلتراسیون، روغن کشی، بسترهای جریان، فرآیندهای بیولوژیکی و شبکه های گاز طبیعی اهمیت زیادی دارد. جریان های متشکل از حباب که یک نوع جریان دوفازی محسوب می شوند در بسیاری از کاربردهای صنعتی مانند مبدل های حرارتی و راکتورهای حباب-ستون به کار گرفته شده اند. علاوه بر این، امروزه مهندسین مکانیک با مطالعه دینامیک و رفتار میکروحباب ها در تلاش اند تا نیروی پسای وارد بر شناورهای دریایی را در حد امکان کاهش دهند که موفقیت در این زمینه منجر به صرفه جویی در زمان و هزینه های حمل ونقل خواهد شد.

بسیاری از پدیده های روزمره در زندگی به نوعی از دیدگاه عملی، مسائل دوفازی یا چند فازی محسوب می شوند. به عنوان مثال حرکت دانه های باران در روزهای بارانی در هوا و شکل ایجادشده برای قطرات باران یا نحوه حرکت موج بر روی سطوح دریا و نحوه شکست آن نمونه ای از مسائل دوفازی است که در طبیعت رخ می دهد.

جریان های دوفازی نه تنها در مسائل طبیعی رخ می دهند، بلکه دارای کاربرد فراوانی در مسائل صنعتی می باشند. یکی از کاربردهای عمده این دسته جریان ها، فرآیند تولید قطره، اسپری و اتمیزه کردن مایعات هست. اسپری کاربردهای متعددی مانند احتراق سوخت مایع در موتورهای احتراق داخلی، توربین های گازی، کوره ها، دیگ های بخار رنگ آمیزی، نقاشی، پوشش سطوح فلزی جهت جلوگیری از خوردگی و یا تغییر خواص فیزیکی، دستگاه چاپ و چاپگر، خنک کردن لوله ها در سوپرهیترهای دیگ بخار، دستگاه های مرطوب کننده هوا و وسایل زیست محیطی دارد. همچنین جریان های دوفازی دارای کاربرد عمده ای در زمینه طراحی راکتورهای هسته ای می باشند. در این راکتورها گرمای ایجادشده توسط شکافت هسته ای باعث گرم شدن سیال اطراف راکتور می گردد که این سیال در اثر گرمای محیط و فشار بالا حالت دوفازی دارد. علاوه بر جریان های فوق این گونه جریان ها محدوده وسیعی از کاربردها در زمینه علوم زیست محیطی، ژئوفیزیک، فیزیک و مهندسی را می پوشاند.

حل عددی مدل های جریان های چند فازی

تقریب های عددی موجود در جریان های چندفازی عبارتند از :

1-تقریب اویلری-لاگرانژی

2- تقریب اویلری – اویلری.

 

تقریب اویلری – لاگرانژی:

در این تقریب فاز سیال به عنوان یک سیال پیوسته درنظرگرفته می شود که به وسیله معادله ناویر-استوکس- زمان متوسط) حل می شود، درحالیکه فاز ذرات به وسیله دنبال کردن توده بزرگی از ذرات، حباب ها و یا قطرات درون میدان جریان محاسبه شده به دست می آید. مومنتم، انرژی و جرم فاز ذرات با فاز سیال مبادله می شوند. فرض اساسی در این مدل این است که فاز دوم ذرات، كسر حجمی کوچکی را اشغال می کند اگرچه می تواند بار جرمی بالایی داشته باشد. در هنگام محاسبات فاز سیال، مسیر ذرات یا قطرات به طور جدا و در مسیرهای متناوب محاسبه می شوند. این مدل برای مدل های خشک کن تزریقی، احتراق و برخی از جریان های مملو از ذرات مناسب است اما برای مخلوط های مایع- مایع، بسترهای سیالی و در هر کاربردی که کسر حجمی فاز دوم غير قابل صرف نظر است مناسب نیست. در مدل فاز مجزا از این نوع تقریب استفاده می شود.

تقریب اویلری – اویلری:

زمانی که حجم یک فاز نمی تواند به وسیله فازهای دیگر اشغال شود مفهوم کسر حجمی بیان می شود. کسر حجمی تابع پیوسته ای از مکان و زمان است که مجموع آن یک می باشد. معادلات بقا برای هر فاز مشتق گیری می شود تا یک سری معادلات بدست آیند که ساختار مشابهی برای همه ی فازها دارند. در ادامه مدل هایی که در آنها از این تقریب استفاده شده است مورد بررسی قرار می گیرد.

مدل های مختلف چند فازی اویلری – اویلری:

در حل عددی سه مدل مختلف چند فازی اویلری- اویلری وجود دارد که عبارتند از :

1- مدل حجم سیال

2-مدل مخلوط

3-مدل اویلری.

 

مدل حجم سیال:

این مدل یک تکنیک تعیین مسیر سطحی است که برای یک شبکة ثابت به کار برده می­شود. این مدل برای دو یا بیش از دو سیال مخلوط­نشدنی طراحی شده است که وضعیت سطح مشترک بین فازها دارای اهمیت می باشد و برای هر فاز اضافه ای که به مدل اضافه می شود یک متغیر معرفی می گردد. در مدل حجم سیال، کسر حجمی هر یک از سیالات در هر سلول محاسباتی از طریق ناحیه محاسباتی ردیابی می شود. در این مدل یک سری منفرد از معادلات مومنتم، به وسیله سیالات، تقسیم شده است و کسر حجمی هریک از سیالات در هر سلول محاسباتی در منطقه دنبال می­شود. کاربردهای این مدل شامل پیشگویی شکست جت، جریان های لایه ای و جریان های سطح آزاد، حرکت حباب ها در یک سیال و در حالت کلی مسیریابی گذرا یا دائم هر فصل مشترک گاز مایع می باشد. از محدودیت های مدل حجم سیال می توان به موارد زیر اشاره کرد:

-باید از حل کننده معادلات مجزا در این مدل استفاده کرد و استفاده از حل کننده معادلات کوپل شده برای این مدل کاربرد ندارد(به دلیل تغییر فاز که منجر به اختلاف چگالی بین دو فاز می شود عملا نمی توان از معادلات کوپل شده برای حل مدل های چند فازی استفاده کرد).

-همه حجم کنترل ها باید با یک فاز سیال واحد یا ترکیبی از فازها پر شوند، به عبارتی دیگر مدل حجم سیال، مناطق خالی که سیالی در آن وجود ندارد را مدل نمی کند.

-جریان باید تراکم ناپذیر باشد یا حداکثر فقط یکی از سیالات می تواند تراکم پذیر باشد.

مدل مخلوط:

این مدل همانند مدل حجم سیال برای دو یا بیش از دو فاز (سیال یا ذرات) طراحی شده است، با این تفاوت که اختلاف سرعت نسبی بین فازهای مختلف نیز درنظرگرفته می شود. مدل مخلوط، با حل معادلات مومنتم، سرعت های نسبی بین فازهای مختلف را تعیین می کند و سپس با حل معادلات پیوستگی، انرژی، اغتشاش و معادلات کسر حجمی، فازهای مختلف مورد بررسی و تحليل قرار می گیرد. کاربرد این مدل برای جریان مملو از ذرات با فشار کم، جریان های شامل حباب، جریان رسوب و جریان های گردابه ای می باشد. مدل مخلوط، همچنین میتواند با درنظرنگرفتن سرعت های نسبی برای فازهای جدا به منظور مدل­کردن جریان چندفازی، از مدل همگن استفاده کند. محدودیت های مدل مخلوط نیز تقریبا همانند مدل حجم سیال است.

مدل اویلری :

این مدل کامل ترین و دقیق ترین مدل در بین مدل های چندفازی می باشد که n معادله مومنتم و پیوستگی را در هر فاز حل می کند. این مدل بین ضرایب تبدیل فاز میانی فشار، ارتباط به وجود می آورد که این ارتباط به نوع فازها بستگی دارد و برای جریان های دانه ای(جامد- سیال) متفاوت با جریان غیردانه­ای (سیال – سیال) است.

تئوری مدل حجم سیال(VOF):

در مدل حجم سیال حرکت ناپایدار فازهای گاز و مایع به وسیله معادله ناویر استوکس و تغییرات موقعیت سطح مشترک گاز مایع که ناشی از حرکت نسبی بین حباب های پراکنده شده و مایع اطراف آن می باشد مورد بررسی قرار می گیرد. این مدل تفاضل محدود که برای اولین بار توسط هیرت و نیکز ارائه شد به دلیل توانایی محاسبه و نمایش بسیار دقیق سطح مشترک گاز – مایع مورد استفاده قرار گرفت. مدل VOF به صورت کسر حجمی یا تابع غلظت C(x,t) تعریف می شود و کسری از پرشدن سلول بوسیله مایع را نشان می دهد. مقدار تابع غلظت بین صفر و یک متغیر است. اگر کل حجم سلول را گاز فرا گیرد این مقدار صفر و اگر کل این حجم را مایع فراگیرد این مقدا یک می باشد.

 

روش پیشروی جبهه(front tracking):

روش حل عددی حاکم بر این پروژه روش پیشروی جبهه است. در این روش سطح مشترک به وسیله یک سری نقاط معين معلوم می گردد. در طول حل، این نقاط به روش لاگرانژی دنبال می شود. در این روش معمولا سلول های محاسباتی برای حل میدان سرعت و فشار به صورت ثابت در کل دامنه قرار دارند و به صورت اویلری درنظر گرفته می شوند. در واقع این روش هر دو خصوصیت روش های اویلری و لاگرانژی را دارد. حسن روش پیشروی جبهه آن است که انحناهایی به مراتب کوچکتر از دقت سلول های محاسباتی را می تواند مدل نماید.

روش های عددی به کار گرفته شده برای شبیه سازی مرز مشترک:

جریان های با سطح مشترک و جریان های سطح آزاد بخش بزرگی از مسایل سیالاتی را به خود اختصاص می دهند و کاربردهای فراوانی در زمینه های مختلف صنعتی، زیست محیطی ، ژئوفیزیک و … دارند. جریانهای با سطح مشترک به آن دسته از جریان ها گفته می شود که دو سیال در یک سطح مشترک با یکدیگر در تماس هستند، نظیر تماس آب و روغن، هوا و سوخت مایع در فرآیندهای احتراقی.

سطح مشترک دو سیال به علت وجود نیروی کشش سطحی و ایجاد پدیده هایی نظیر ناپایداری کلوین-هلمولتز و ناپایداری ریلی تیلور از پیچیدگی زیادی برخوردار است. همچنین به دلیل متحرک بودن سطح مشترک و پیچیدگی شکل سطح که می تواند به شدت با زمان تغییر کند، این مساله از لحاظ عددی نیز از پیچیدگی های خاصی برخوردار است. در چنین جریان هایی سطح مشترک را می توان یک سطح درنظرگرفت که خواص سیال نظير فشار و چگالی در دو طرف آن متفاوت بوده و به صورت توابعی ناپیوسته هستند. در حالت حدی، جریان با مرز مشترک به جریان با سطح آزاد تبدیل می شود. در این حالت یکی از فازها با فرضيات ساده کننده ای مدل می شود. به طور کلی روش های شبیه سازی جریان با مرز مشترک متحرک به دو دسته زیر تقسیم می شوند:

1-روش های دنبال کردن مرز مشترک (روش لاگرانژی)

2-روش های تسخیر مرز مشترک(روش اویلری).

یک روش مناسب برای شبیه سازی سطح مشترک باید دارای معیارهای زیر باشد:

 1-بقای جرم را رعایت کند.

 ۲-حداقل از دقت مرتبه دوم باشد.

3-ضخامت سطح را تا حد امکان کوچک محاسبه کند.

4-قابل تعمیم به مسایل سه بعدی باشد.

5-به محاسبات زیاد نیاز نداشته باشد.

 

روش های دنبال کردن مرز مشترک(interface tracking):

این روش ها ماهیتی لاگرانژی دارند یعنی سطح توسط نقاطی مشخص می گردد و با ردیابی این نقاط سطح ردیابی می شوند. در این روش در هر مرحله چهارچوب مرجع بایستی دوباره بررسی و شناخته شود و شبکه­بندی مجدد، مقداردهی دوباره نقاط را به همراه دارد که می تواند بسیار پیچیده باشد. به عبارت دیگر در روش لاگرانژی دقت کاهش می یابد. در جریان با مرز مشترک، اگر یک جریان برگشتی داشته باشیم و یا اگر جابه جایی سیال شدید باشد، برای مثال مرز مشترک گسسته یا شکسته شود، این روش ها کمتر مفید خواهند بود. تعدادی از روشهایی که تابحال ابداع شده اند و اساس آنها در ردیابی سطح به شرحی که در بالا گفته شد استوار است، عبارتند از روش های جابه جایی سلول های محاسباتی، روش انتگرال سلول های مرزی و روش ذرات.

روش جابه جایی سلول های محاسباتی(moving mesh method):

در این روش سلول های محاسباتی با حرکت مرز مشترک سیال به نحوی جابه جا می شوند که همواره سلول هایی که در یک سیال واقع شده اند، در همان سیال باقی بمانند. با این تفسیر نتیجه می شود که سلول ها در طول حل عددی همیشه دارای خاصیت های فیزیکی ثابت هستند. از این رو حل معادلة ناویر استوکس به آسانی در هر کدام از دامنه ها صورت می گیرد و عدم پیوستگی در خصوصیات سیال در مرز مشترک دقیقا رعایت می شود. مشکل اصلی این روش آن است که پس از گذشت زمان، شکل المان های دامنه محاسباتی برای حل معادلات ناویر استوکس نامناسب می گردد و باید دامنه حل دوباره شبکه بندی شود.

این مشکل هنگامی جدی تر می گردد که سطح انحنای شدید یا شکست یا ترکیب را در حل مساله دوفازی داشته باشیم که در این صورت لازم است گام های زمانی به شدت کم و عملیات شبکه بندی پیاپی انجام گردد.

روش انتگرالی سلول های مرزی(boundary integral method):

این روش تنها از المان های مرزی برای مدل کردن دامنه حل استفاده می کند. مهم ترین حسن این روش کاهش قابل توجه هزینه های محاسباتی است بدین صورت که به اندازه یک مرتبه بعد مساله را کاهش میدهد. به عنوان مثال برای حل مسایل سه بعدی تنها یک سطح و برای مدل سازی یک سطح تنها خط مرز مشترک را حل می کند. مشکل اصلی این روش آن است که مسایلی را می تواند حل کند که حالت خطی داشته باشند. در نتیجه درمسایل سیالات این روش مسایلی را می تواند حل کند که عدد رینولدز به سمت صفر یا بی نهایت میل کند. بنابراین این روش جامعیتی برای حل مسایلی که در رینولدز محدود رخ می دهد، ندارد.

روش های تسخیر مرز مشترک(interface capturing):

این دسته از روش ها به روش های اویلری معروفند. به این معنی که شبکه محاسباتی در تمام مدت حل ثابت و بدون تغییر باقی می ماند و سیال درون شبکه حرکت می کند. دامنه کاربرد روش های اویلری نسبت به روش های لاگرانژی گسترده تر است و می توان پدیده هایی نظیر شکست سطح یا به هم پیوستن سطح را شبیه سازی کرد. این روش برای مدلسازی سطح مشترک به طور مستقیم مرز مشترک را دنبال نمی کند بلکه با نسبت دادن یک تابع به المانها سعی می کند به صورت غیر مستقیم مكان سطح مشترک را دنبال کند. از جمله مهم ترین روش های اویلری می توان به روش لول ست و کسر حجمی سیال اشاره نمود.

روش کسر حجمی سیال:

این روش یکی از روش های بسیار معروف در دینامیک سیالات محاسباتی برای حل مسایل با سطح آزاد یا مسایل سیالات دوفازی به شمار می آید. این روش بر پایه بقای جرم است. در حل مسایل سیالات دو فازی روش کسر حجمی سیال بدین صورت است که به سیال اولی عددی دلخواه مثلاً یک و به سیال دومی عدد صفر را نسبت می دهند. در نتیجه در هر المانی که سیال اول وجود داشته باشد، آن المان مقدار یک را به خود اختصاص خواهد داد و هر المان که تنها شامل سیال دوم باشد، عدد صفر را به خود تخصیص می دهد و در المان هایی که مقداری از سیال اول و مقداری از سال دوم موجود باشد، عددی بین صفر و یک را به خود اختصاص خواهد داد. عدد نسبت داده شده به سلول ، نسبت حجم اشغال شده توسط سیال اولی به حجم کل المان است. با این نوع تخصيص دهی کل دامنه محاسباتی شامل المان هایی خواهد شد که دارای عددهای بین صفر و یک هستند.

این مساله که مقدار کسر حجمی در طول دامنه حل ثابت است، به صورت ریاضی در دیدگاه اویلری به شکل Dc/Dt=0  نشان داده می شود. این معادله اصلی روش کسر حجمی سیال است که با حل این معادله در زمان می توان مقدار را در طول زمان به دست آورد. درنتیجه با دانستن مقدار c، می توان محل سطح مشترک را تشخیص داد. برای پیش برد c در طول زمان می توان از روش نیمه لاگرانژی استفاده کرد. با توجه به این که برای بازسازی سطح مشترک تنها یک عدد و در اختیار است، اولین روش های به وجود آمده توسط روش کسر حجمی سیال، روش هایی مرتبه اول بودند که از توابع مرتبه یک برای تشکیل سطح مشترک استفاده می کردند. روش های مرتبه دوم به روش های PLIC مشهور هستند. در این روش ها علاوه بر معین نمودن مقدار کسر حجمی سیال می توان جهت نرمال سطح مشترک را به کمک معین نمودن جهت عمود بر سطح مشترک پیدا نمود.

روش لول ست (Level set):

معادله لول ست اولین بار برای مدلسازی سیالات تراکم ناپذیر چند فازی معرفی شد. به علت قدرت این روش در دنبال کردن سطوح مشترک، این روش نه تنها برای مدلسازی سیالات تراکم ناپذیر چند فازی بلکه برای بررسی مسایل سیالات تراکم پذیر، برای مدلسازی شعله با سرعت پایین ، انفجار و احتراق و سیالات با سطح آزاد مورد استفاده قرار گرفت. یکی از مشکلات عمده روش لول ست از دست دادن جرم در طول انجام محاسبات است. معادله لول ست را بدون در نظر گرفتن تمهیدات خاصی می توان از یک روش اویلری پیشرونده در طول زمان و یک تابع بالا دست برای گسسته سازی جمله جابه جایی معادله لول ست استفاده نمود. به دلیل وجود شرط محدودساز CFL برای این روش، هزینه محاسباتی آن زیاد است. یکی از علت های ایجاد این ناپایداری عدم باقی ماندن تابع لول ست به صورت یک تابع فاصله است. در این راستا معادلات دوباره مقدار دهی به وجود آمدند. هدف از این معادلات رعایت تابع فاصله توسط تابع لول ست است.

فرض کنید که سرعت در هر نقطه از فضا به کمک تابع برداری V(x) داده می شود و همچنین فرض بر آن است که تابع سرعت در تمام نقاط مقدار مشخص و معلومی دارد. فصل مشترک دو سیال که در حالت کلی به صورت یک سطح است، به کمک تابع (x) ϕ معرفی می گردد.

 

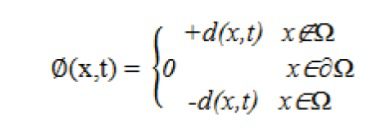
 برای این منظور به سطح مشترك عدد صفر و به سیال درون فاز اول، مقدار منفی و به سیال بیرونی، مقادیر مثبت نسبت داده می شود که اندازه این مقادیر متناسب با کمترین فاصله از سطح مشترک است. مطابق شکل:

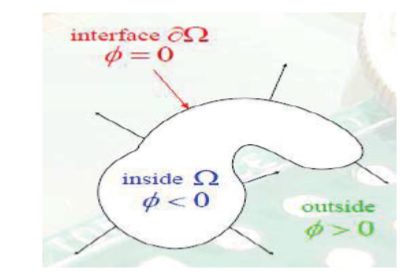
شکل نحوه توزیع تابع سطح تراز در داخل و خارج مرز مشترک.

 

از آنجا که سطح مشترک با تابع 0= (x) ϕ معین شده است و در طول زمان نیز این مقدار نباید تغییر بکند درنتیجه می توان معادله را به شکل لاگرانژی نوشت:

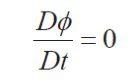
این رابطه بیانگر مشتق کامل است، اگر آن را بر حسب متغیرهای اویلری بنویسیم :

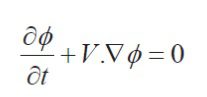
این معادله به معادله لول ست معروف است. در حالت کلی برای به دست آوردن مکان سطح مشترک تنها اطلاعات سرعت بر روی محدوده سطح مشترک مورد نیاز است ولی معمولا در معادلات مکانیک سیالات میدان سرعت در تمام دامنه حل موجود است.

روش عددی پیشروی جبهه در محاسبات جریان های چند فازی:

در این روش کلیه معادلات حاکم برای یک سیال، که خود دارای خواص فیزیکی متغیر است، پایه ریزی می­شود. در واقع فرض می گردد که در کل دامنه حل یک سری از معادلات باید حل شوند منتها خواص فیزیکی در این دامنه متفاوت است. که همین متفاوت بودن خواص فیزیکی مرز بین دو سیال را مشخص می­کند. در معادلات جمله هایی که مربوط به مرز مشترک بین دو فاز هستند به صورت توابع دلتا و به شکل یک جمله چشمه به معادلات اضافه می شوند. معادلات ناپایای ناویر استوکس توسط گسسته سازی اختلاف محدود روی یک شبکه ثابت حل می شوند و مرز مشترک دو فاز توسط نقاط و المان های شماره دار به صورت مستقیم ردگیری می شوند. در این روش از یک شبکه ثابت سازمان یافته اویلری برای حل میدان جریان و یک شبکه متحرک برای ردیابی مرز مشترک استفاده می شود که شبکه متحرک دارای یک بعد کمتر از ابعاد شبکه ثابت است. در این جا چون شبکه ثابت دوبعدی است بنابر این مرز مشترک با شبکه متحرک باید به صورت یک بعدی باشد. این موضوع در شکل زیر کاملا مشهود است.

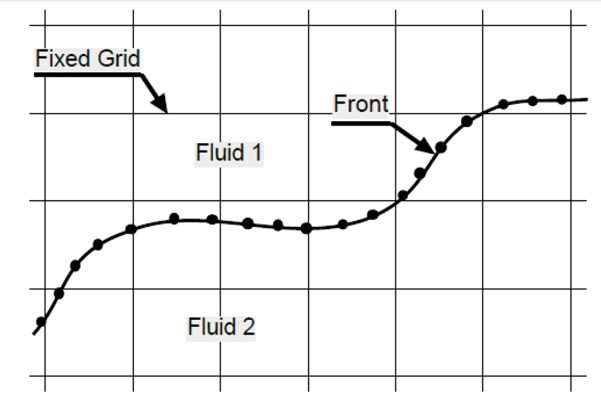
شكل نحوه قرار گیری دو سیال مختلف در کنار هم و ساختار مرز مشترک.

در این روش از یک سری از معادلات برای کل دامنه حل استفاده می شود که باید جمله های چشمه مناسبی برای محاسبه برخی از کمیت ها در مرز مشترک، به این معادلات اضافه شوند. این جمله ها که فقط در مرز مشترک مقدار دارند و در بقیه نواحی دامنه وجود ندارند توسط توابع دلتا به معادلات اصلی اضافه می­شوند. وقتی هر یک از جملات معادلات برای حل عددی گسسته سازی می شود این جمله ها نیز باید همچون دیگر جمله ها با یک سری از عبارات تقریب زده شوند.

ساختار مرز مشترک دو فاز:

ساختار مرز مشترک بین دو فاز که در این جا به علت دو بعدی بودن مساله، به صورت یک منحنی است، از چندین نقطه و المان تشکیل شده است. این نقاط مرز مشترک را به تعداد زیادی خط های کوچک تقسیم می کنند که به هر یک از این خطوط، المان می گویند(مطابق شکل زیر). این نقاط و المان ها شماره گذاری شده و به صورت یک آرایه ذخیره می شوند و هرکدام از آنها با نقاط و المان های بعدی و قبلی در ارتباط اند. این آرایه ها کار را برای حذف و اضافه کردن نقاط و المانها راحت تر می کنند.

این موضوع در شکل زیر پیدا است. هرکدام از نقاط ذخیره شده دارای مختصات مخصوصی هستند که در آرایه ها ذخیره می شوند. همچنین هر المانی دارای اطلاعات نقاطی که به آن متصل است، خواهد بود. هرکدام از این المان ها دارای جهت مخصوص به خود هستند و بردار نرمال آنها با توجه به مختصات نقاط ابتدایی و انتهایی آنها مشخص است. همه این مطالب برای المان های سه بعدی نیز صادق است با این تفاوت که المان های کنار یکدیگر از جنس سطح هستند نه خط.

شكل نقاط و المان های سازنده مرز مشترک در (الف) دوبعد (ب) سه بعد.

 

بازسازی مرز مشترک(interface reconstruction):

ممکن است با حرکت مرز مشترک بعضی از نواحی دارای تراکم زیاد نقاط و المان ها و در دیگر نواحی این تراکم کمتر باشد. برای دقت بیشتر در حرکت مرز مشترک و حفظ شكل دقيق آن باید در نواحی که تعداد المان ها یا نقاط زیاد است بعضی از آنها را حذف کرد و بالعکس اگر در جایی از مرز تراکم نقاط و المان ها کمتر است باید تعدادی نقاط و المان به آن اضافه کرد. به طور کلی بعد از هر بار حرکت مرز مشترک یک توزیع یکسان روی مرز مشترک باید برای نقاط و المان های سازنده مرز مشترک صورت بگیرد. همچنین برای جلوگیری از تشکيل زوایای تند و تیز مرز که باعث به وجود آمدن گرادیانهای فشار بالا می شوند از یک تابع هموار ساز بر روی نقاط مرز مشترک استفاده می شود. البته می توان این هموار سازی را بعد از تعداد گام زمانی مشخصی روی مرز اعمال کرد.

روش ردیابی جبهه:

در روش ردیابی جبهه کلیه معادلات حاکم بر روی یک شبکه اویلری ثابت، با شبکه بندی یکنواخت حل می گردند. اما به جهت تشخیص هر کدام از فازهای موجود از خواص فیزیکی متفاوت استفاده می شود. در واقع می توان این گونه گفت که تشخیص همین مرز بین دو فاز موجود و اعمال خواص فیزیکی مربوط به هر کدام از فازهای موجود نکته مهم روش ردیابی جبهه است.

هنگامی که قرار بر آن است تا مرز مشترک دو فاز را ردیابی نماییم، درواقع با دو شبکه کار داریم. بدین صورت که یک شبکه مربوط به حل معادلات حاکم بر سیال است و شبکه دیگر با یک بعد کمتر از شبکه اصلی مربوط به ردیابی و پیش بینی مکان مرز مشترک دو سال است. همان طور که در شکل زیر دیده می شود، شبکه منظم و ثابت برای محاسبه و ترسیم میدان سرعت و فشار، و شبکه جبهه برای حرکت مرز مشترک دو فاز در محيط حل و به دست آوردن مقدار تنش سطحی است.

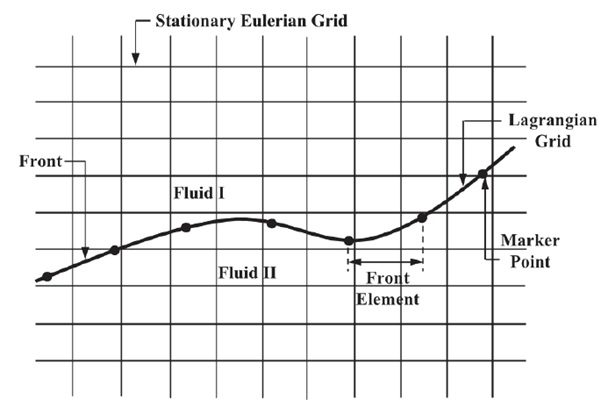
شکل شبكه حل میدان سرعت و فشار (شبکه اویلری) و شبکه مرز مشترک ( جبهه).

کلید حل این روش، همانند دیگر روش های عددی برای مدل سازی جریان چندفازی، استفاده از یک دسته معادلات حاکم برای کل سیال است. بعلاوه برای بررسی تفاوت خواص مواد در هر کدام از فازهای مختلف سیال، ما باید پدیده های مربوط به سطح مشترک دو سیال را از قبيل تنش سطحی، وارد مسئله نماییم.

 

شرح پروژه:

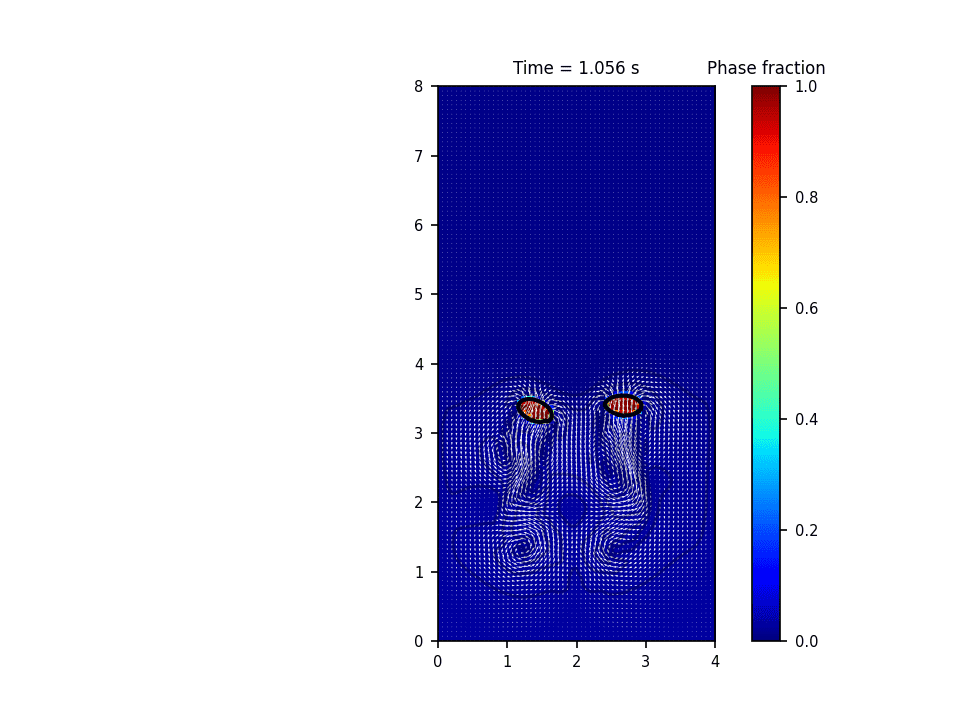
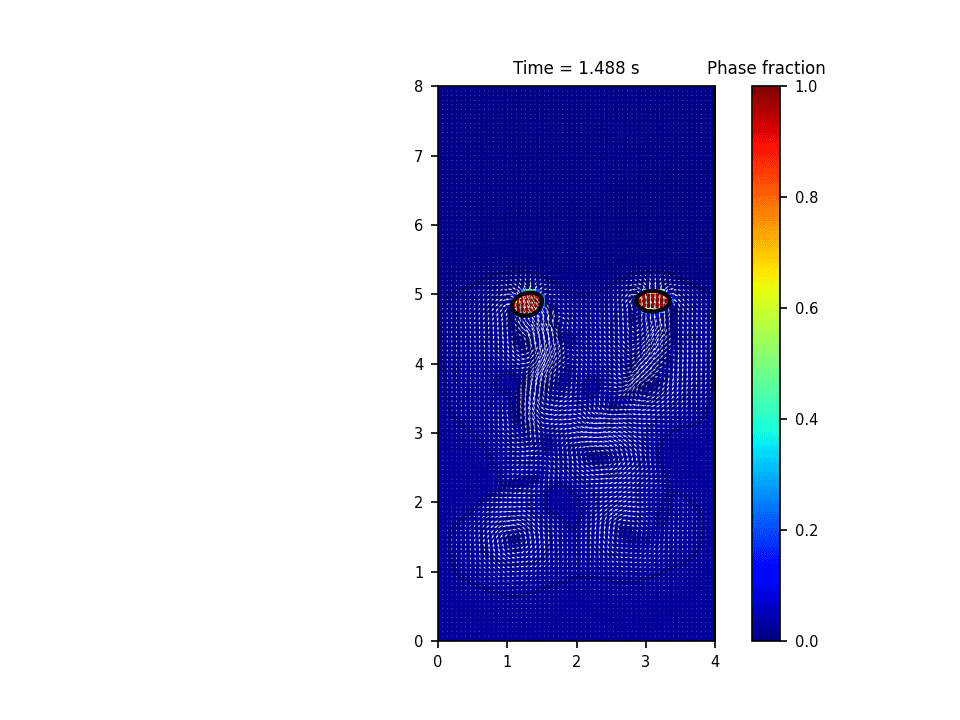
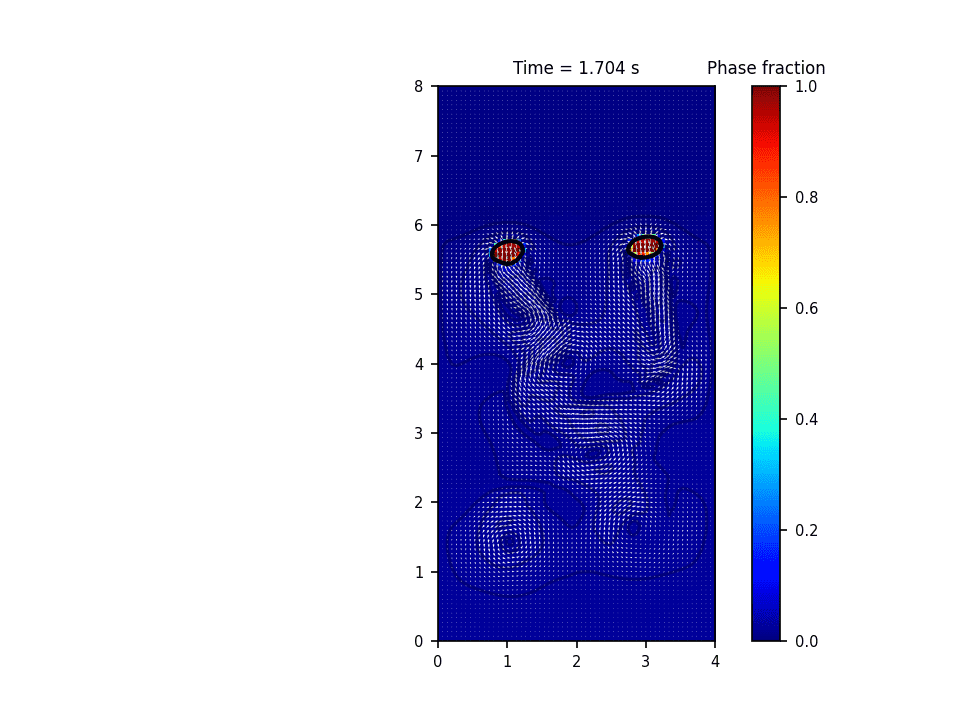
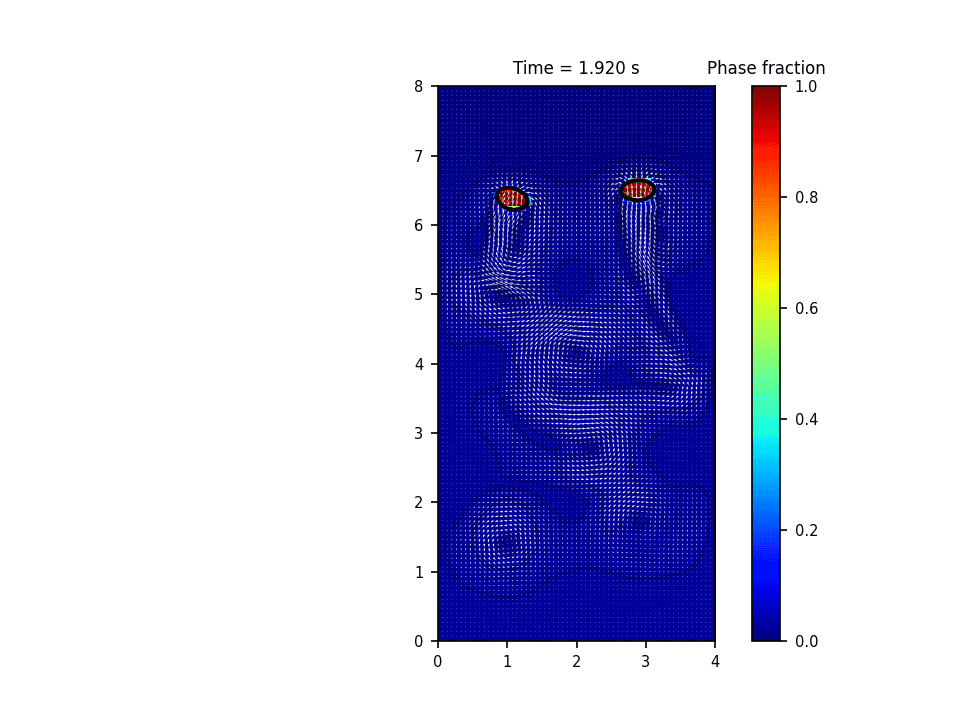
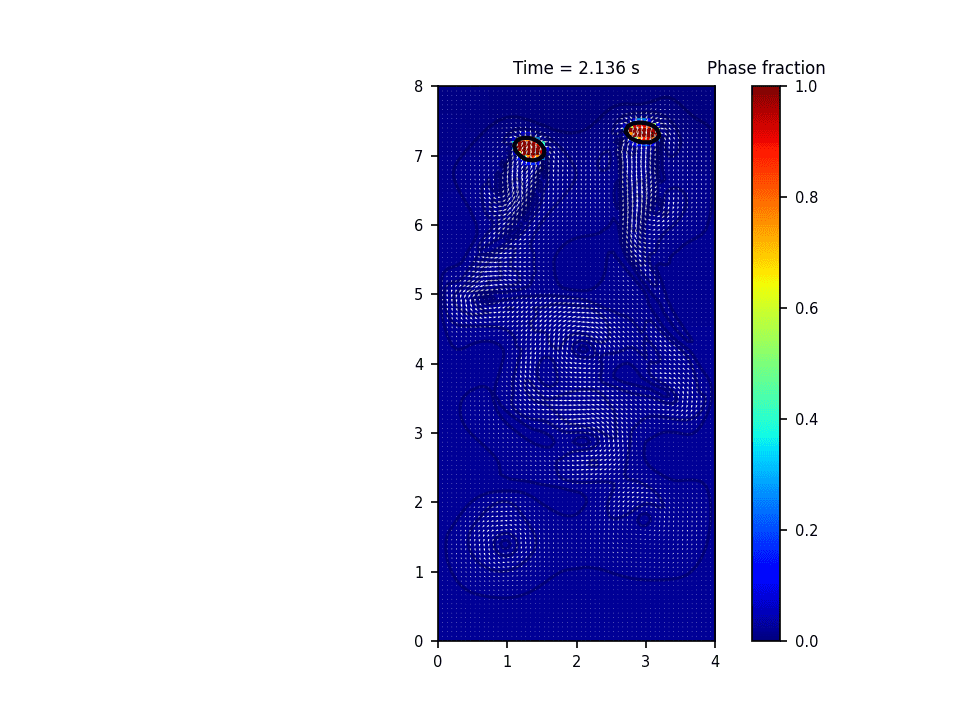
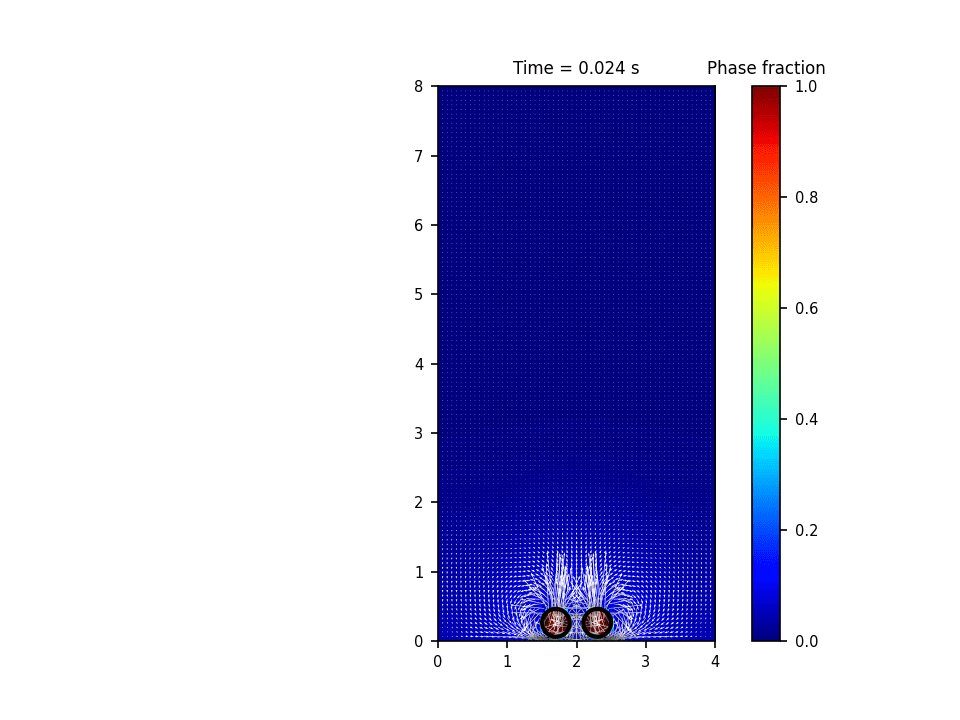
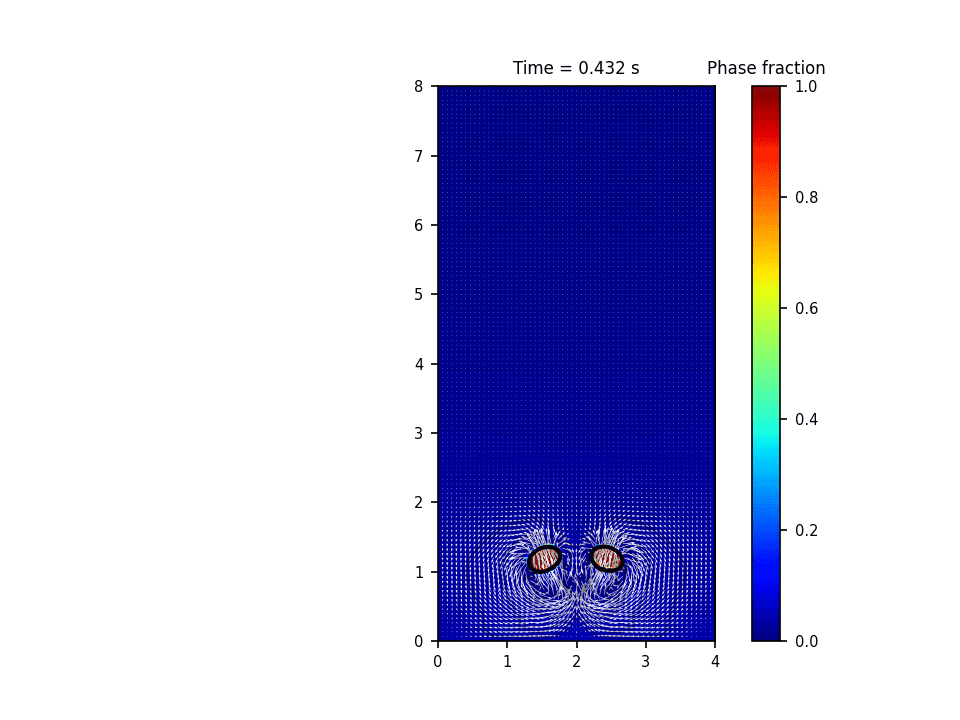
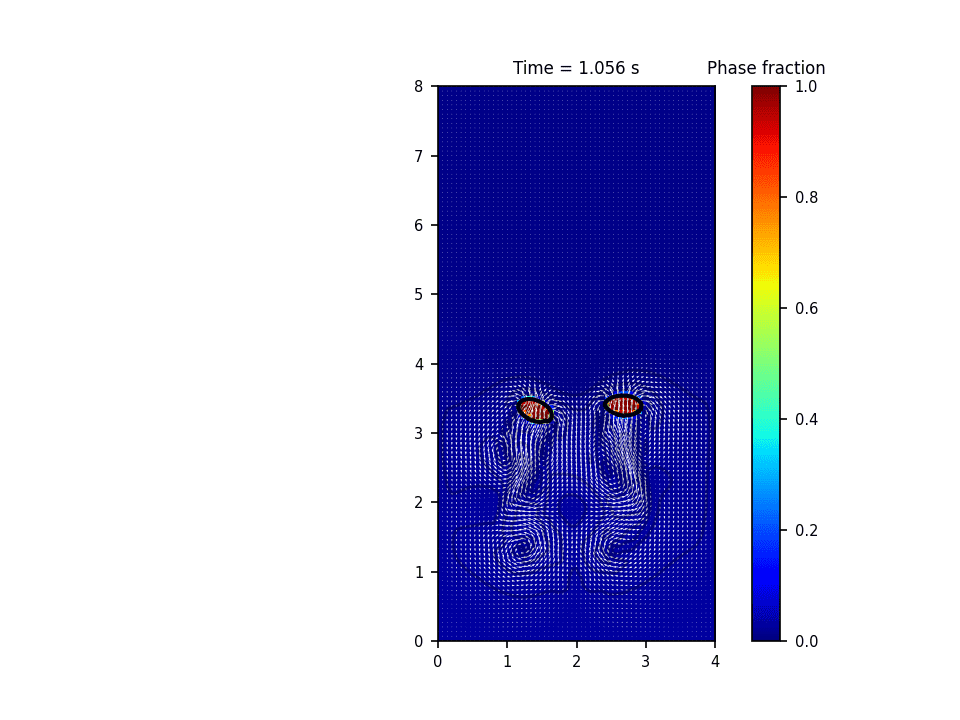
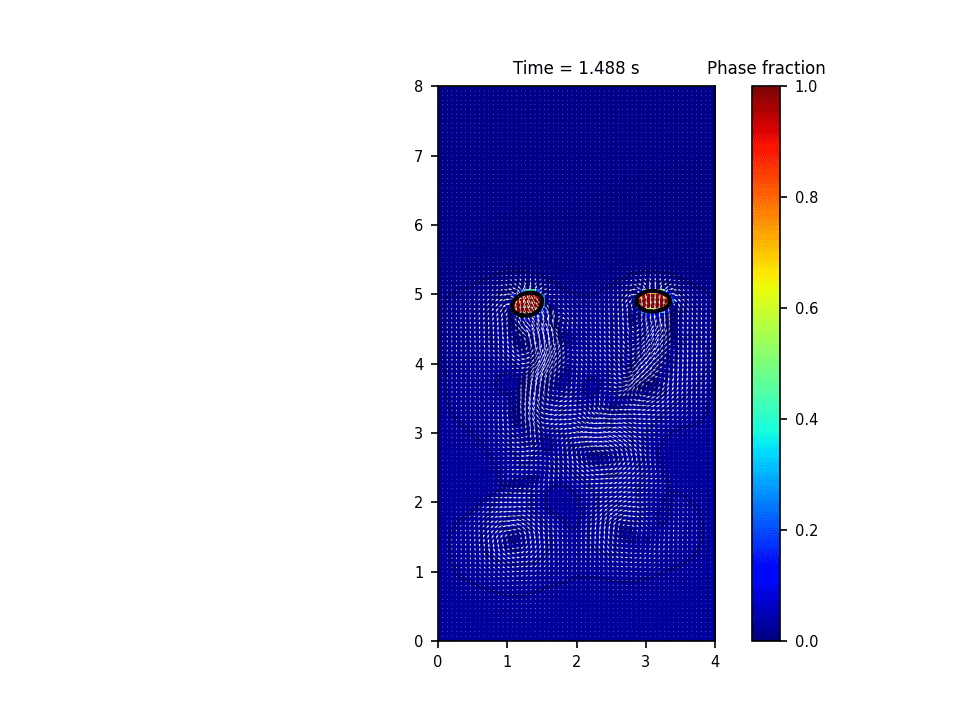
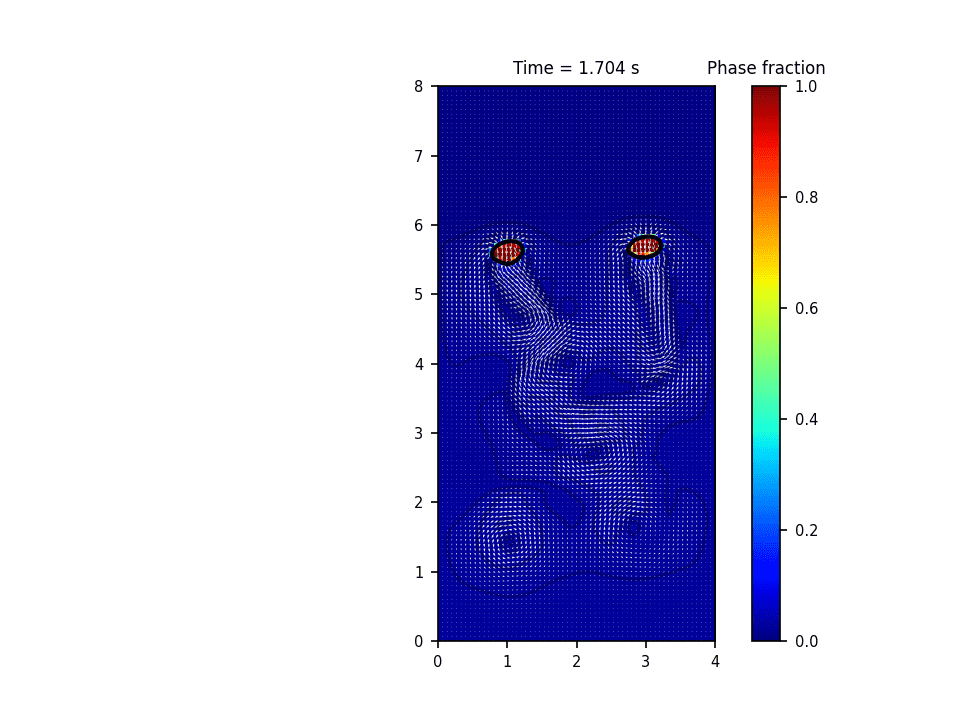
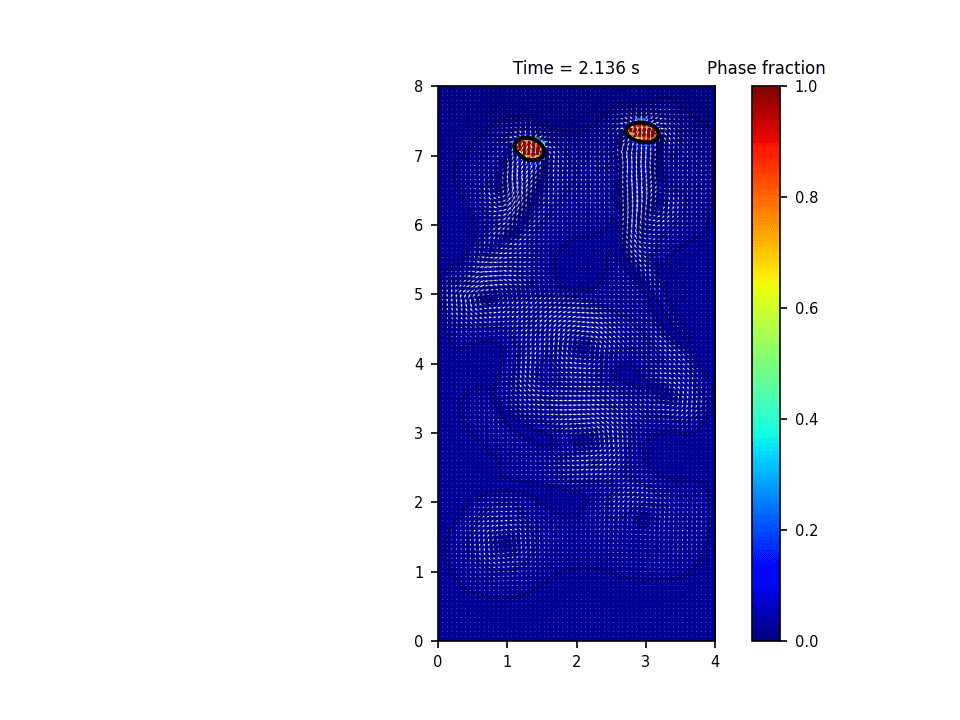
روش حل عددی حاکم بر این پروژه روش پیشروی جبهه(front tracking) برای تشکیل و صعود حباب(bubble rise) می­باشد. در این روش سطح مشترک به وسیله یک سری نقاط معين معلوم می گردد. در طول حل، این نقاط به روش لاگرانژی دنبال می شود. در این روش معمولاً سلول های محاسباتی برای حل میدان سرعت و فشار به صورت ثابت در کل دامنه قرار دارند و به صورت اویلری درنظر گرفته می شوند. در واقع این روش هر دو خصوصیت روش های اویلری و لاگرانژی را دارد. حسن روش پیشروی جبهه آن است که انحناهایی به مراتب کوچکتر از دقت سلول های محاسباتی را می تواند مدل نماید.

نتایج شبیه سازی در نرم افزار پایتون: