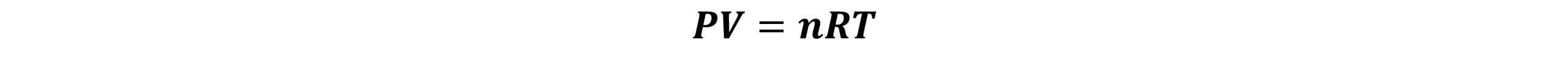توضیحات
تخمین حجم ویژه گاز متان در یک مخزن به کمک معادله حالت ردلیچ-وانگ(RK) و روش تکراری نیوتن رافسون در نرم افزار متلب(MATLAB)
شرح پروژه:
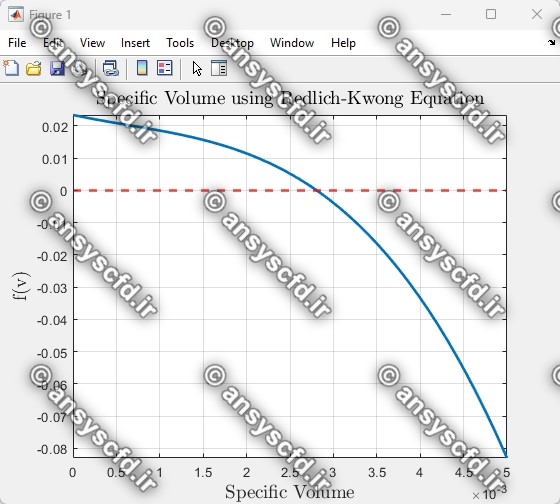
در این پروژه تخمین حجم ویژه گاز متان(m3/kg) و همچنین جرم متان در یک مخزن به کمک معادله حالت ردلیچ-وانگ(RK) و روش تکراری نیوتن-رافسون(Newton-Raphson) در نرم افزار متلب(MATLAB) کدنویسی شده است. حجم مخزن 3 مترمکعب و دمای آن 40- درجه سانتیگراد در فشار 65000 کیلوپاسکال می باشد.
گازها:
گازها را بهصورت مجموعهای از مولکول ها (یا اتمها) میتوان درنظرگرفت که به صورت دایم و نامنظم در حرکت هستند. گازها به دو دسته ایده آل و حقیقی تقسیم میشوند، که دارای چهار متغیر فشار (P)، حجم (V)، دما (T) و تعداد مولها (n) هستند. باید رابطهای بین چهار متغیر وجود داشته باشد. قانون ساده گازها رابطه بین دو متغیر را وقتی که دو متغیر دیگر ثابت باشند، بیان میکند. طبق قانون بویل- ماریوت وقتی تعداد مولها و دما ثابت باشد، فشار با حجم به نسبت عکس تغییر میکند. قانون شارل- گیلوساك بیان میکند که در فشار و تعداد مولهای ثابت، حجم یک گاز با دمای آن نسبت مستقیم دارد و همچنین در حجم و تعداد مول های گازی ثابت، فشار آن گاز با دما نسبت مستقیم دارد. معادله حالت یک گاز کامل، رابطه بین چهار متغیر را بهصورت زیر بیان میکند:
در این معادله، R ثابت گاز میباشد. هر گازی که از این معادله تبعیت کند گاز کامل یا ایده آل است. اما برای گاز کامل تعریف مناسبتری نیز وجود دارد. گاز کامل گازی است که:
الف) حجم اشغال شده توسط خود مولکول های گاز (حجم خودی یا حجم مستثنی شده) قابل صرفنظر یا به عبارتی صفر باشد.
ب ) نیروهای بین مولکولی(شامل نیروهای جاذبه و دافعه) صفر باشد.
هر عاملی که گازها را به این دو شرط اساسی نزدیک کند باعث نزدیکی گازها به حالت ایده آل میشود. مثلاً افزایش حجم، افزایش دما، کاهش فشار و کاهش چگالی یا تراکم مولکول ها یا غلظت. در شرایط دما و فشار معمولی، گازهای حقیقی به طور نسبتاً کامل از قوانین گاز ایده آل پیروی میکنند. ولی در دمای پایین یا فشارهای بالا یا هر دو مورد گازهای حقیقی از گازهای ایده آل انحراف نشان میدهند. علل انحراف از حالت ایده آل نیروهای بین مولکولی و حجم مولکول هاست.
مایعات:
مایع ماده ای است که آزادی حرکت مولکول های آن بیشتر از جامدات اما کمتر از گازهاست. ذرات ریزی که مایعات را تشکیل میدهند نسبت به جامدات انرژی بیشتر، اما نسبت به گازها انرژی کمتری دارند. مایعات این تفاوت را نیز با گازها دارند که نمیتوان آنها را با فشرده کردن در فضای کوچکی جای داد. میزان مقاومت یک مایع در مقابل جاری شدن ویسکوزیته خوانده میشود. مایعات غلیظ مانند قیر ویسکوزیتهی بالایی دارند و به کندی جاری میشوند، اما مایعات رقیق مانند آب ویسکوزیتهی پایینی دارند و به راحتی جاری میشوند. کشش سطحی موجب میشود که سطح مایعات مانند نوعی پوسته عمل کند. این کشش توسط نیروهای بین مولکولهای مایع، که آنها را کنار هم نگه میدارد ایجاد میشود. در زیر سطح، مولکولهای مایع از همه طرف توسط مولکولهای دیگر احاطه شده اند، بنابراین این نیروها یکدیگر را خنثی میکنند. اما در سطح مایع، مولکولها فقط از سه طرف احاطه شده اند. این عدم تعادل، مولکول های سطح را به سمت درون میکشد و پوسته مایع را تشکیل میدهند. قطرات و حبابهای آب به دلیل کشش سطحی گرد هستند. مولکولهای سطح به سمت داخل کشیده میشوند و یک شکل کروی را تشکیل میدهند.
نظریه حالت مایع به اندازه گازها پیشرفت نکرده است و توسعه معادلات عمومی برای توصیف رفتار حجمی فاز مایع خیلی ترقی نکرده است ولی در شرایط عمومی دما و فشار، حجمهای مایعات را میتوان بهصورت تجربی بهدست آورد، البته فشار و دما و بهخصوص فشار، تأثیر نسبتًا کمی روی حجم مایع به جز در نواحی بحرانی دارد.
انواع معادلات حالت(Equation of state):
برای بیان توضیح دقیقی از رفتار PVT سیالات در دامنهی وسیعی از دما و فشار، به یک معادله حالت جامع احتیاج است. البته نباید این معادله آن قدر پیچیده باشد که مشکلات عددی یا تحلیلی اضافهای را در کاربردش به وجود آورد. از سادهترین معادلاتی که قادر به بیان رفتار مایع و بخار میباشد میتوان به معادلههای چند جملهای اشاره کرد که در آنها حجم مولی از نوع درجه سوم است.
معادله حالت گاز کامل تنها در محدوده کوچکی از دما و فشار یک گاز حقیقی قابل استفاده است، به همین منظور برای توصیف سیالات در محدوده های وسیعتر معادلههای حالت تجربی و شبه تجربی که نتایج بهتری دارند پیشنهاد و ارایه شدند.
معادلههای حالت را میتوان به سه گروه تقسیمبندی کرد: ١ – تجربی، 2- نیمهتجربی، 3- نظری.
اغلب معادلههای حالت نیمهتجربی هستند و ضرایبی که در آنها گنجانده شده، از طریق اطلاعات تجربی بهدست میآید.
معادلات حالت تجربی:
این معادلات عموماً شامل تعداد زیادی از پارامترهای ویژه با معنای فیزیکی کم هستند. اما با اینحال با داده های تجربی مطابقت داشته و بهطور نوعی برای یک سیال خاص یا گروه کوچکی از سیالات طراحی شدهاند. این دسته از معادلهها برای سیال مورد نظر خود، تحت شرایط مربوطه با دقت بالایی عمل میکنند.
معادلات حالت نیمهتجربی:
معادله حالتهای نیمه تجربی از ادغام محاسبات نظری و دادههای تجربی حاصل میشوند. معادلههای نیمهتجربی معمولاً دقت زیاد و کاربردهای فراوانی دارند. معادله حالت واندروالس یکی از معادلات حالت نیمه تجربی می باشد که در ادامه به آن اشاره می شود.
معادله حالت واندروالس(Van der Waals):
این معادله اولین معادله درجه سوم عمومی حالت است که توسط واندروالس در سال 1873 پیشنهاد شد.
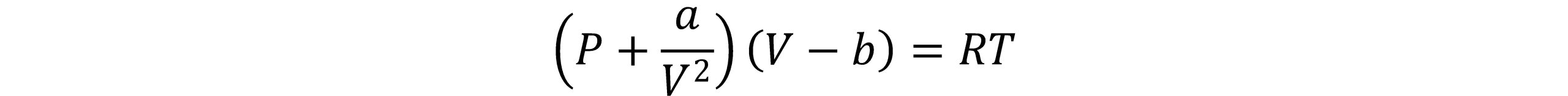
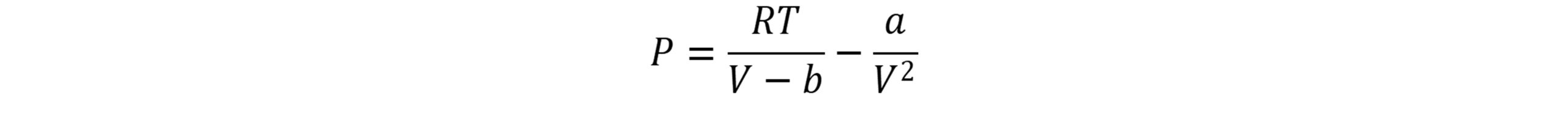
در این معادله P فشار، T دما، V حجم، n تعداد مول ها و R ثابت جهانی گازها است. مقدار ثابت b برای تصحیح حجم اشغال شده توسط مولکول ها و عبارت a/V2 تصحیح لازم برای نیروهای جاذبة بین مولکولی است.
a و b می توانند با اعمال شرایط نقطه بحرانی سیالات حاصل شوند:
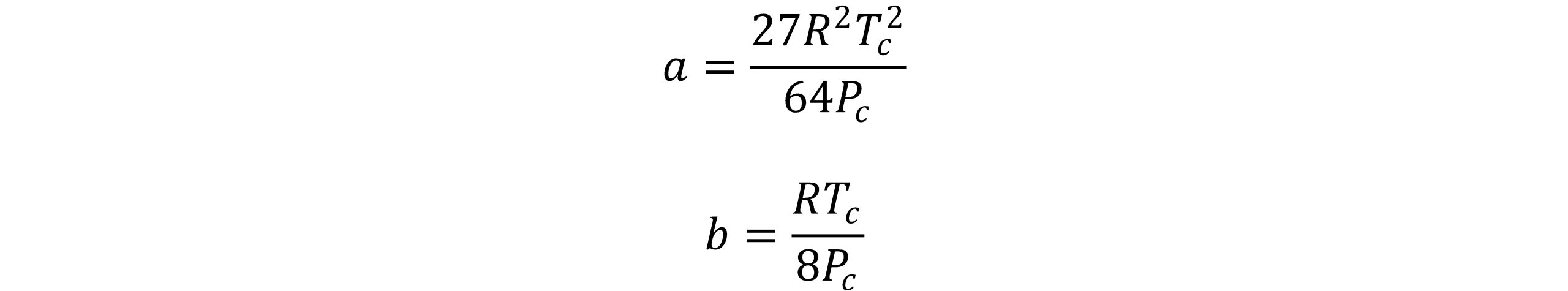
این معادله توسط افراد زیادی تصحیح و به معادله حالتهای بهتری تبدیل شده است.
معادله حالت ردلیچ- وانگ(RK)
این معادله حالت تا حد قابل توجهی دقیقتر از معادلهی واندروالس است. معادلهی RK توسط ردلیچ و وانگ در سال١٩٤٩پیشنهاد شد. آنها در این معادله، عبارت مربوط به دافعه را در معادله حالت واندروالس بدون تغییر نگه میدارند ولی وابستگی دمایی را در عبارت جاذبه وارد کردند.این معادله حالت به صورت زیر نشان داده شده است.
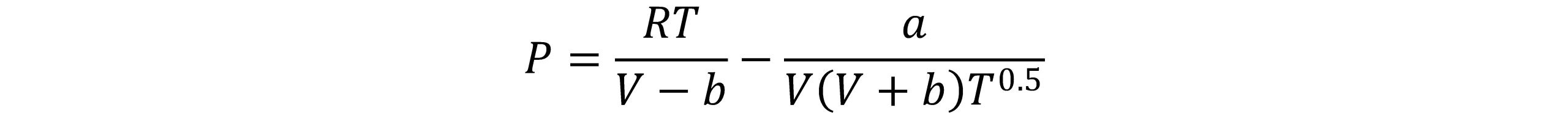
در این رابطه پارامترهای a و b برای مواد خالص به صورت زیر تعریف می شود:
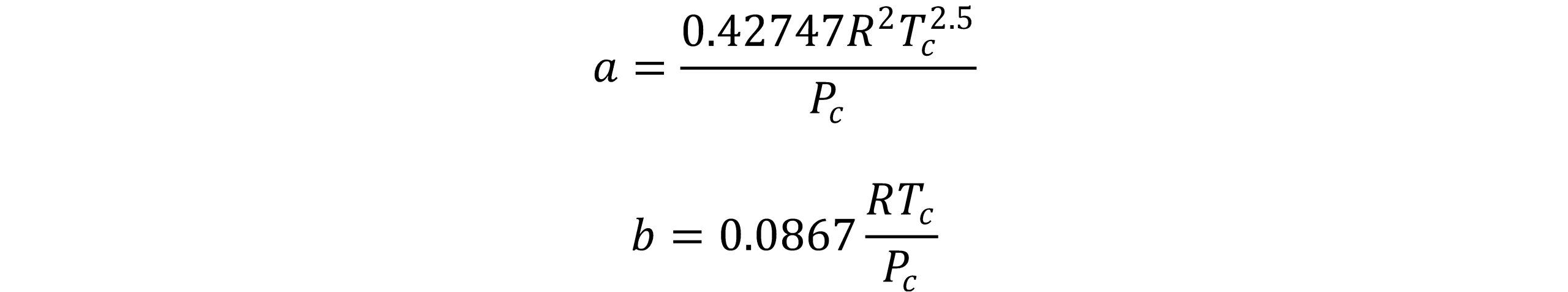
معادله RK در ناحیه وسیعی از فشار و دما از دقت بالایی برخوردار است و در محاسبات مربوط به مخلوط های دو جزئی و خصوصیات بحرانی نقطه دو فازی بخار- مایع با موفقیت مورد استفاده قرار میگیرد. برخی از حالتهای اصلاح شده این معادله در سال های اخیر کاربرد پیدا کرده اند.
نمونه نتایج: