توضیحات
حل معادله دیفرانسیلی معمولی(ODE) با روش رانگ-کوتا مرتبه چهار(RK4) و مقایسه با اویلر صریح و ضمنی در نرم افزار متلب(MATLAB)
شرح پروژه:
در این پروژه حل معادله دیفرانسیل معمولی زیر با روش رانگ-کوتا مرتبه چهار(RK4) در نرم افزار متلب(MATLAB) کدنویسی شده است و با روش های اویلر ضمنی و صریح مقایسه گردیده است. معادله دیفرانسیل معمولی مرتبه اول زیر را درنظر بگیرید.
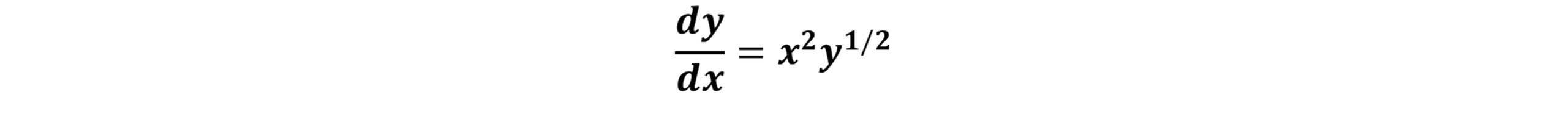
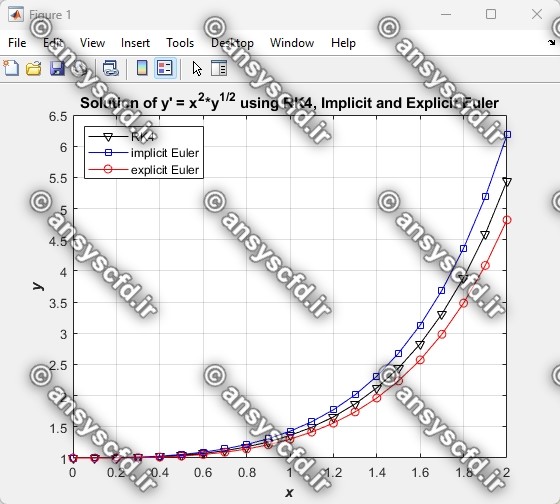
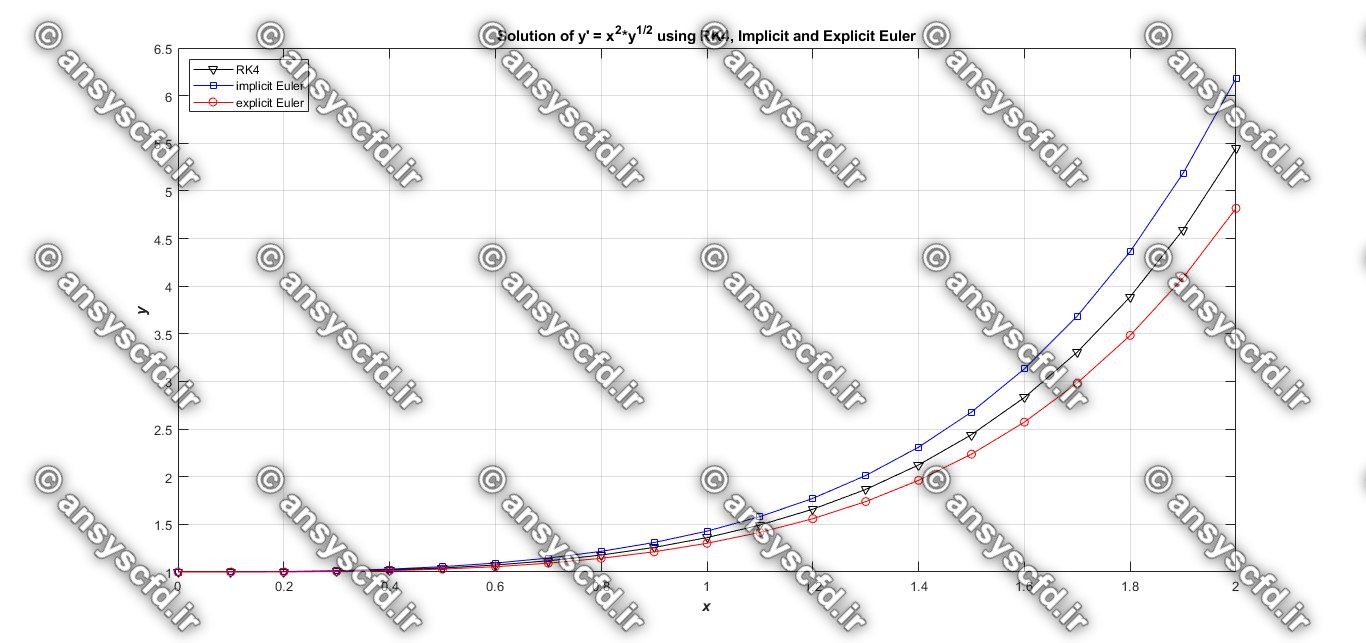
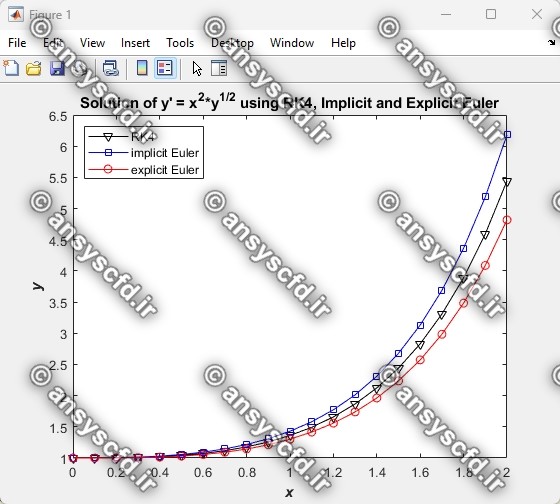
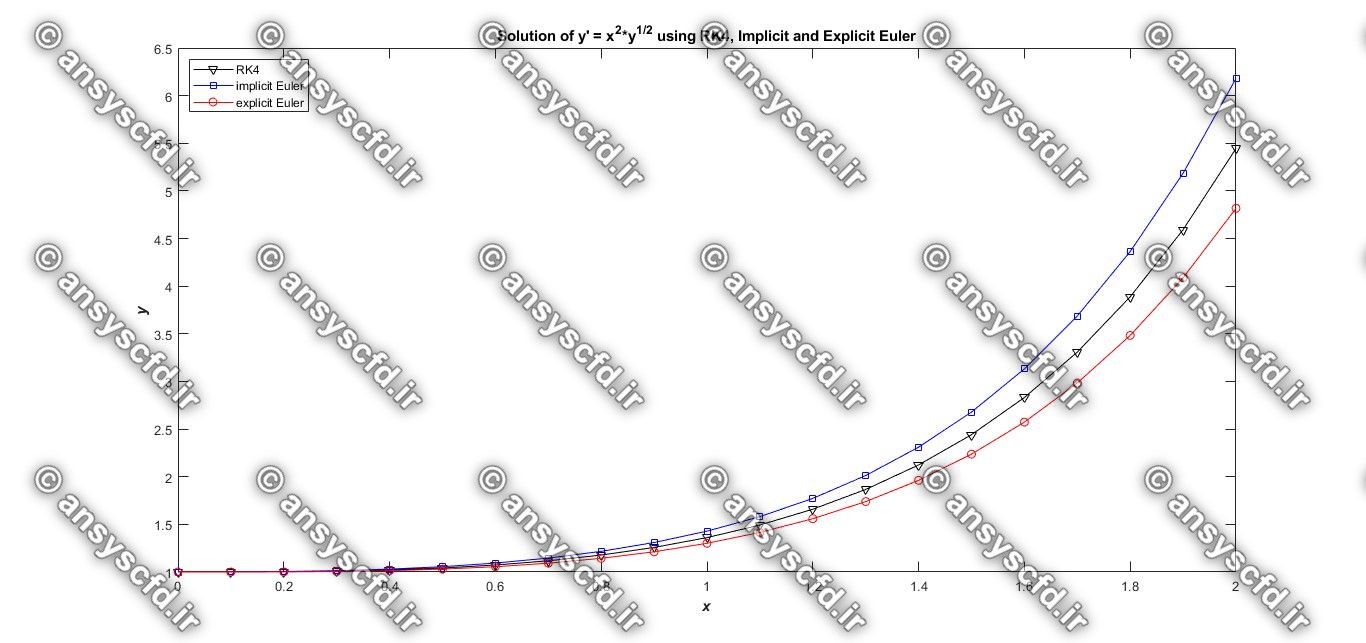
شرط اولیه در نقطه 1= (0)y داده شده است. مطلوب است حل معادله(ODE) مرتبه اول با روش رانگ-کوتا مرتبه چهار(RK4) با گام 0.1 در فاصله [0.2, 0] و با روش های اویلر صریح و ضمنی مقایسه کنید.
معادله دیفرانسیل معمولی:
یک معادله دیفرانسیل معمولی(ODE) رابطه ای بین یک تابع مجهول یک متغیره، مشتق های تابع و متغیر مستقل می باشد. یک معادله دیفرانسیل معمولی معادله ای است از یک تابع مجهول و مشتقات آن که صورت کلی یک معادله دیفرانسیلی معمولی(ODE) به صورت زیر بیان می شود:
![]()
در رابطه فوق x متغیر مستقل بوده و y متغیر وابسته می باشد. جواب این معادله دیفرانسیلی معمولی(ODE) به صورت یک تابع y(x) می باشد که در معادله دیفرانسیلی صدق کند که این y را جواب معادله دیفرانسیلی می نامیم. یک معادله دیفرانسیل همیشه جواب یکتا ندارد. برای اینکه این معادله یک جواب یکتا داشته باشد نیاز به شرایط اولیه و مرزی داریم. اگر یک معادله دیفرانسیلی تنها یک متغیر مستقل داشته باشد آن را یک معادله دیفرانسیلی معمولی(ODE) می نامیم و معادله ای که دارای مشتقات جزئی بوده که لزوماً شامل چند متغیر مستقل است را معادله دیفرانسیلی پاره ای یا جزئی(PDE) می نامیم.
مسائل مقدار اولیه و مسائل مقدار مرزی:
مسائل مقدار اولیه (IVP) : مقادیر متغیر مستقل و مشتق های آن در یک نقطه خاص معلوم است. یک معادله دیفرانسیلی معمولی همراه با شرایط اولیه را مسئله مقدار اولیه می گویند.
مسائل مقدار مرزی(BVP): مقادیر متغیر مستقل و مشتقات آن در نقاط متفاوت در دامنه حل معلوم می باشد. یک معادله دیفرانسیل معمولی همراه با شرایط مرزی را مسئله مقدار مرزی می گویند.
معادلات دیفرانسیل معمولی براساس مرتبه مشتق موجود در معادله تقسیم می شوند. بالاترین مرتبه مشتق معادله نشان دهنده مرتبه معادله دیفرانسیلی است.
معادله دیفرانسیلی معمولی مرتبه اول:
شکل کلی معادله دیفرانسیلی معمولی مرتبه اول به صورت زیر بیان می شود:
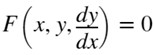
با شرط اولیه y (x=x0)= y0 .
برای اکثر مسائل فیزیکی، معادله دیفرانسیل معمولی با مسئله مقدار اولیه به شکل زیر می باشد.
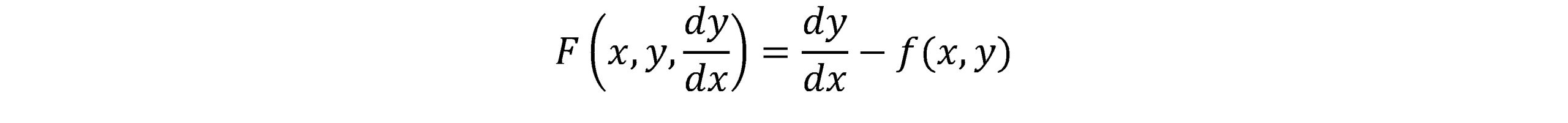
بنابراین می توان نوشت:
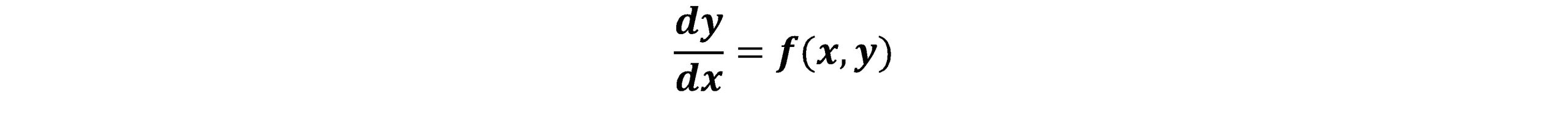
روش اویلر صریح(Explicit Euler):
روش اویلر صریح، ساده ترین روش تقریب عددی برای حل مسائل مقدار اولیه(IVP) می باشد که در آن مشتق را با یک روش تفاضل پیشرو تقریب می زند. درواقع در روش اویلر مقدار جدید(yi+1) باتوجه به مقدار قبل و گام حل با فرض تقریب مرتبه اول محاسبه می شود.
معادله این روش به صورت زیر بیان می شود:
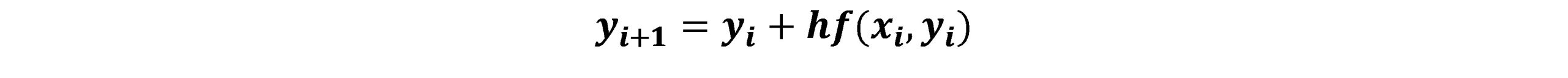
در رابطه فوق، h اندازه گام تکرار می باشد و اشاره به نمو بین دو مقدار متوالی دارد.
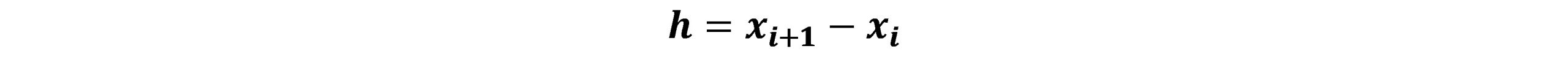
روش اویلر ضمنی(Implicit Euler):
در روش اویلر ضمنی، مشتق در مقادیر جدید به کمک تقریب تفاضل محدود پسرو ارزیابی می شود. طرح اویلر ضمنی به صورت زیر بیان می شود:
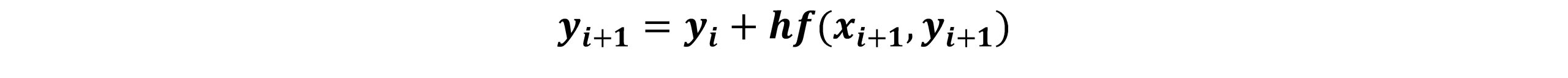
همانطور که در رابطه فوق مشاهده می شود، تنها اختلاف روش اویلر ضمنی با اویلر صریح این است که تابع سمت راست در زمان جدید f(yi+1) ارزیابی می شود. اغلب اوقات yi+1 را نمی توان به صورت صریح محاسبه نمود. بایستی توجه داشت که رابطه فوق یک رابطه غیرخطی برحسب yi+1 است که برای حل آن بایستی صفر تابع و ریشه های تابع را با یکی از روش های عددی مانند روش نیوتن محاسبه کنیم. بنابراین بایستی آن را از حل معادله جبری زیر محاسبه نمود.
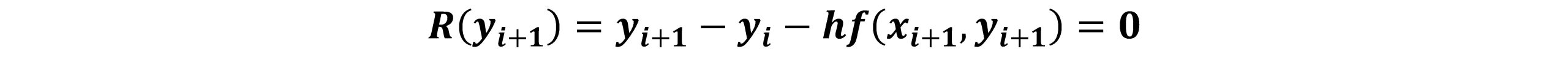
رابطه فوق بطورکلی غیرخطی است. روش انتخاب برای حل این معادله روش نیوتن است که بایستی در هر مرحله از انتگرال گیری اعمال شود. واضح است که پیاده کردن و حل معادله دیفرانسیلی با روش اویلر ضمنی دشوارتر از روش اویلر صریح است. مزیت روش اویلر صریح این است که بی قید و شرط پایدار است. حال قصد داریم معادله دیفرانسیلی معمولی(ODE)، y’=x2y1/2 را با استفاده از روش اویلر ضمنی حل نماییم. رابطه اویلر ضمنی بر حسب ریشه معادله به صورت زیر بیان می شود:
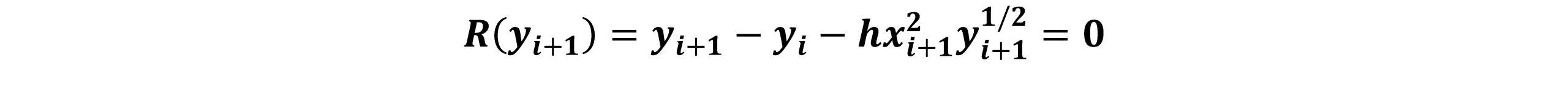
برای حل متغیر مجهول yi+1 با استفاده از روش نیوتن، با حدس اولیه yi+1(0) شروع کرده و از رابطه تکراری زیر yi+1 را محاسبه می کنیم.
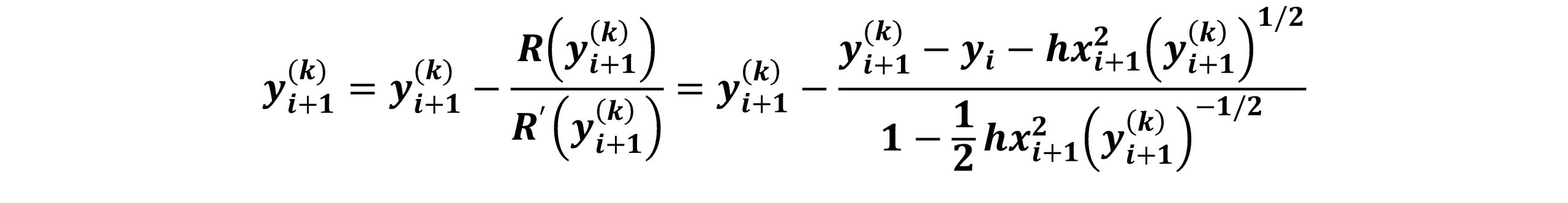
روش رانگ-کوتا:
روش های رانگ-کوتا (Runge-Kutta) برای تقریب های مرتبه بالاتر طراحی شده اند بطوریکه به محاسبه مشتقات بالاتر نیازی نباشد. روش رانگ-کوتا در مقایسه با روش اویلر که یکبار تابع f را محاسبه می کند، در هر مرحله چندین بار این تابع محاسبه می شود. در این روش از یک ترکیب خطی از f برای محاسبه شیب استفاده می شود. پرکاربردترین روش رانگ-کوتا، روش رانگ-کوتا مرتبه چهار می باشد. فرمولاسیون این روش به صورت زیر است:
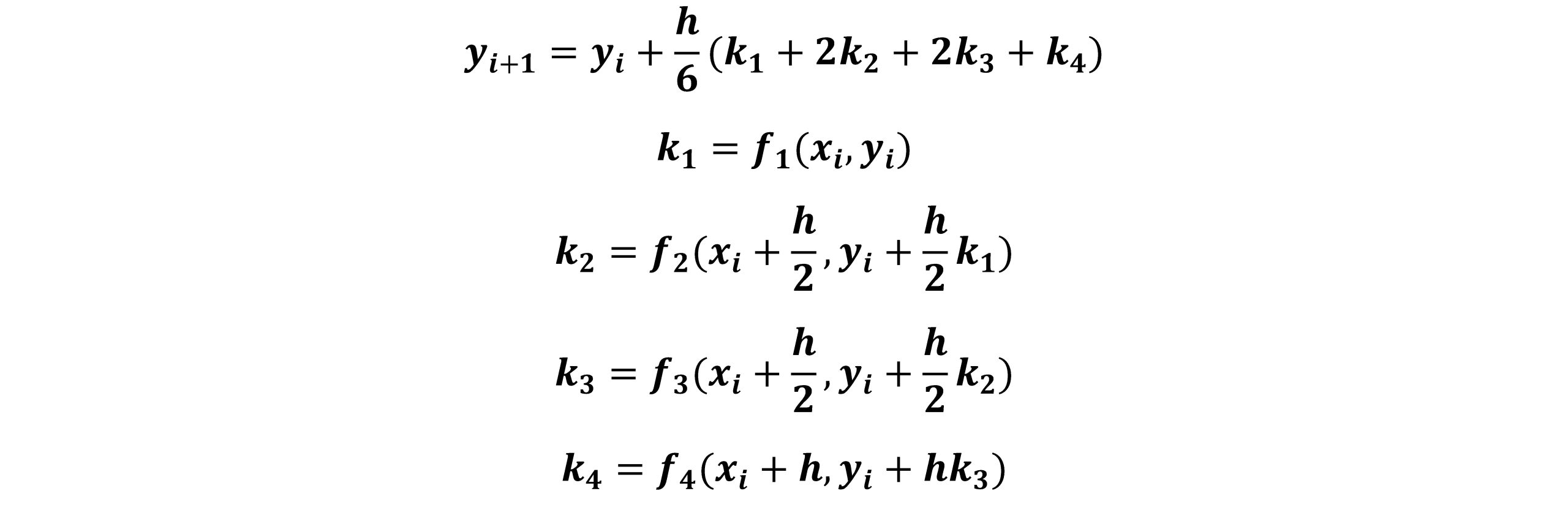
نمونه نتایج: