توضیحات
پروژه متلب حل پخش بار اقتصادی با الگوریتم شیرمورچه چندهدفه(MALO)

الگوریتم شیر مورچه(ALO):
یکی از تکنیک ها در مسائل بهینه سازی، الگوریتم ALO می باشد. یک الگوریتمALO از نحوه شکار شیرمورچه و به دام افتادن مورچه در تله آن الهام می گیرد. نام گذاری این الگوریتم به دلیل نوع خاص شکارکردن و طعمه مورد علاقه آن می باشد. شیر مورچه ها تله خود را به صورت گودال مخروطی شکل می سازند. در شکل زیر چند نمونه تله با اندازه های مختلف نشان داده شده است.

شکل تله های ساخته شده توسط شیر مورچه.
بعد از حفر تله، شیر مورچه ها در پایین گودال به انتظار شکار می نشینند. شکل زیر چگونگی کمین نشستن شیر مورچه ها را نشان می دهد.

شكل نحوه به دام افتادن مورچه ها.
تله ها به گونه ای بنا شده اند که هنگامی که مورچه ای در آن گرفتار می شود با شیب خیلی زیادی روبرو می شود. از طرفی به محض اینکه شیر مورچه از حضور مورچه در تله آگاه می شود، با استفاده از چنگک هایی که بر روی فکش واقع شده است، تمامی سعی خود را برای شکار مورچه می کند. با این وجود مورچه همچنان به تلاش خود برای فرار از تله ادامه می دهد و در این زمان شیر مورچه دانه های ماسه را به طرف لبه گودال پرتاب می کند. زمانی که مورچه شکار می شود شیر مورچه آن را به زیر گودال می کشد و بعد از مصرف، اضافی آن را به بیرون از تله پرتاب می کند.
عملکرد الگوریتمALO:
الگوریتم ALO از عکس العمل بین شیر مورچه ها و مورچه های در تله افتاده استفاده می کنند. برای مدلسازی تعاملات، ابتدا مورچه را به عنوان حرکت در فضای جستجو در نظر می گیریم، سپس شیر مورچه مجاز به شکار آن می شود. از آنجایی که مورچه به صورت تصادفی در محل می رود، حرکت مورچه ها طبق رابطه زیر مدل شده است:

که cumsum مجموع تجمعی را محاسبه می کند. n نشان دهنده بیشترین تکرار، t بیانگر مرحله راه رفتن تصادفی است(t-امین تکرار در این زمان)، r(t)- تابع تصادفی است که به شکل زیر در می آید.
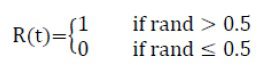
به طوری که t بیانگر مرحله قدم زدن تصادفی و rand عدد تصادفی در بازه [0,1] دارد. موقعیت مورچه ها در ماتریس زیر ذخیره و در طول بهینه سازی مورد استفاده قرار می گیرد:

به طوری که Mant موقعیت هر مورچه را مشخص می کند، Aij مشخص کننده jامین متغیر i-امین مورچه است. n مشخص کننده تعداد مورچه ها و d مشخص کنندهی تعداد متغیرها است. مورچه ها همانند ذرات در الگوریتمPSO و افراد در الگوریتمGA می باشد. موقعیت مورچه پارامترها را برای راه حل خاص بیان می کند. برای ارزیابی هر مورچه، یک تابع برازندگی در طول بهینه سازی مورد استفاده قرار می گیرد. سپس این توابع به شکل زیر ذخیره می شوند:
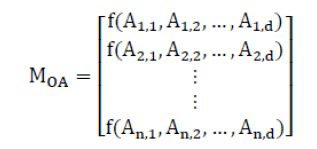
MOA به منظور ذخیره سازی مقدار تابع برازندگی هر مورچه استفاده می شود. فرض می کنیم شیر مورچه ها در فضایی پنهان شده باشند. به منظور ذخیره این موقعیت و تابع هدف آن ماتریس های زیر مورد استفاده قرار می گیرد:

Mantlion و MOAL به ترتیب مشخص کننده ماتریس موقعیت و ماتریس تابع هدف هر شیر مورچه می باشد. همچنین ALi,j مقدار بعد j ام شیر مورچه i-ام، n تعداد شیرمورچه ها و d تعداد متغیرها را نشان می دهد.
در طول بهینه سازی مراحل زیر اعمال می گردد:
- مورچه ها در سرتاسر فضای جستجو به صورت تصادفی حرکت می کنند.
- راه رفتن تصادفی به همه ی ابعاد از مورچه ها اعمال می شود.
- راه رفتن تصادفی تحت تاثیر تله های شیر مورچه ها قرار می گیرد.
- شیر مورچه ها می توانند متناسب با تابع هدف خود گودال های بزرگتری حفر کنند (هرچه تابع هدف بزرگتر باشد، گودال نیز بزرگتر است).
- شیر مورچه با داشتن گودال بزرگتر، قابلیت گرفتن مورچه های بیشتری را دارد.
- هر مورچه می تواند توسط یک شیر مورچه شکار شود
- محدوده راه رفتن مورچه به صورت انطباقی رو به دام های شیر مورچه کاهش می یابد.
- اگر مورچه ای توسط یک شیر مورچه شکار شود به معنی گرفتن و زیر ماسه بردن مورچه توسط شیر مورچه است.
- بعد از هر بار شکار، شیر مورچه برای گرفتن مورچه بعدی، موقعیت خود را تغییر می دهد و یک گودال با تغییرات مناسب ایجاد می کند.
حرکت تصادفی مورچه ها بر پایه معادله زیر صورت می گیرد.
در هر مرحله از بهینه سازی، مورچه ها با قدم زدن تصادفی موقعیت خود را بروز می کنند. از آنجا که هر فضای جستجو دارای محدودیتی است (دامنه متغیرهای رابطه فوق نمی تواند به طور مستقیم برای بروزرسانی موقعیت مورچه ها قرار گیرد. به منظور قدم زدن تصادفی مورچه ها در فضای جستجو، آن ها توسط معادله زیر نرمال می شوند.

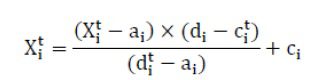
که ai بیانگر مینیمم حرکت تصادفی متغیر در i-امین متغیر است. همچنین bi ماکسیمم حرکت تصادفی متغیر نام است. cit مینیمم i-امین متغير در t- امین تکرار و dit ماکسیمم i-امین متغیر در t- امین تکرار است. معادله فوق باید در هر تکرار انجام شود تا تضمین کننده رخ دادن حرکت تصادفی در فضای جستجو باشد.
باتوجه به مطالب بیان شده قدم زدن مورچه تحت تاثیر تله های شیر مورچه قرار می گیرد. به منظور بیان ریاضی آن مدل زیر بیان می شود:
به طوریکه ct مینیمم مقدار تمامی متغیرها در تکرار t-ام است و dt بیانگر برداری شامل ماکسیمم تمامی متغییرها در تکرار t-ام می باشد. همچنین cit مینیمم مقدار تمامی متغییرها در i-امین مورچه می باشد و dit بیانگر برداری شامل ماکسیمم تمام متغیرها برای i-امین مورچه است. در این معادله Antlionjt نشان دهنده موقعیت j- امین شیر مورچه در t-امین تکرار است. برای مدل کردن توانایی شکار شیر مورچه ها، از ساختار چرخ گردان استفاده می شود. الگوریتمAIO نیاز به یک اپراتور چرخ گردان برای تعیین شیر مورچه ها بر پایه تابع برازندگی آنها در طول بهینه سازی دارد.
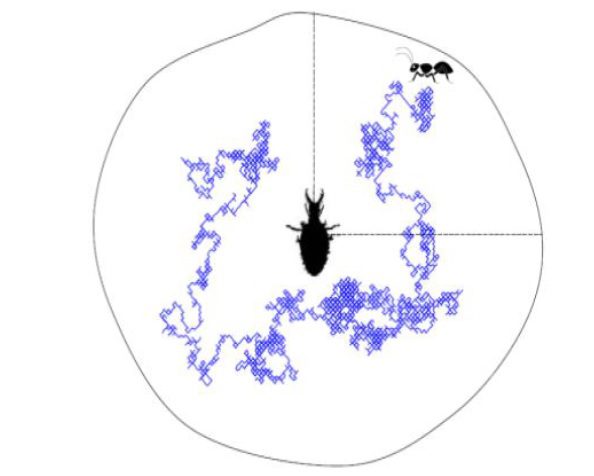
شکل حرکت تصادفی یک مورچه در تله شیر مورچه.
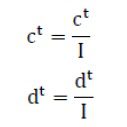
که در این معادله Iیک نسبت ثابت و ct مینیمم تمامی متغیرها در t-امین تکرار، همچين dt شامل برداری با ماکسیمم مقدار متغیرها در t-امین تکرار است و به صورت رابطه زیر تعریف می شود.
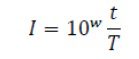
کهt تکرار در حال انجام و T ماکسیمم تعداد تکرارها و w ثابتی است که بر پایه تکرار در حال اجرا بصورت زیر تعریف می گردد.
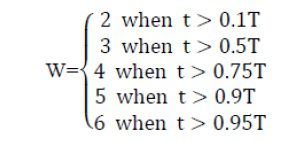
مرحله آخر شکار هنگامی است که طعمه به پایین دام می رسد و در دهان شیر مورچه قرار می گیرد. پس از این مرحله شیر مورچه طعمه را به داخل ماسه می کشد و می خورد. در استفاده از این فرآیند فرض می شود که شکارهنگامی انجام می گیرد که مورچه داخل ماسه فرورفته باشد. سپس می بایست موقعیت شیر مورچه نسبت به موقعیتی که مورچه را شکار کرده است، برای افزایش شانس شکار جدید بروزرسانی شود. رابطه زیر این عمل را بیان می کند:
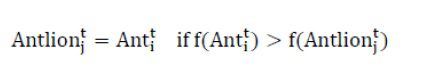
که t نشان دهنده تکرار اجرا است. Antlionjt مرقعیت شیر مورچه j-ام در تکرار t-ام و Antit نشان دهنده مورچه i-ام در تکرار t-ام است.
روش الگوریتم شیرمورچه در حل مسائل بهینه سازی:
الگوریتم ALO در مرحله اول یک جمعیت اولیه از مورچه ها را تولید می نماید و این امر بدین معناست که یک مجموعه راه حل های کاملا تصادفی برای حل مسئله بوجود آمده است. در مرحله دوم مشخص می نماید که مقادیری که به موقعیت مورچه داده شده، درست می باشد یا خیر. در مرحله سوم که مهمترین بخش یک الگوریتمALO است، محاسبه تابع برازندگی مورچه صورت می گیرد که تابع شایستگی یک مورچه نشان میدهد این راه حل تا چه اندازه بهینه می باشد.
پس از آن که میزان تابع برازندگی هر مورچه بدست آمد، در مرحله چهارم، مورچه ها را بر اساس مقدار تابع برازندگی شان، از برازنده ترین تا نامناسب ترین مرتب نموده و در مرحله پنجم بهترین ها به عنوان نخبه در نظرگرفته می شود. در مرحله ششم و هفتم بر روی مجموعه مورچه ها عملگرهای پرش و جهش را اعمال می نماییم.
یک ضریب احتمال هم برای جهش و هم برای پرش در نظر گرفته شده است که بیانگر میزان به کار گیری این عملگرها بر روی جمعیت می باشد. مثلا ضریب 0.9 برای عملگر جهش بدین معناست که بر روی 0.9 جمعیت مورچه ها این عملگر اعمال می گردد. بر روی جمعیت جدید نیز مراحل ۲ و ۳ اعمال گردیده و سپس این جمعیت جدید را به انتهای جمعیت قبلی اضافه می نماییم. حال از عملگر انتخاب، برای گزینش بهترین مورچه ها استفاده نموده و مورچه ای که، بالاترین میزان نخبگی را دارا می باشد، انتخاب می گردد. این روال آنقدر ادامه می یابد که به نرخ قابل قبولی از تشخیص وجود هدف دست یافته باشیم که در این صورت مورچه ای که بعد از اتمام این فرآیند دارای بالاترین میزان تابع برازندگی باشد، به عنوان نخبه ترین مورچه انتخاب می گردد و راه حلی که این مورچه ارائه می دهد، به عنوان بهترین جواب مسئله در نظر گرفته می شود و در واقع این مورچه بهترین پیکربندی حسگرها را با توجه به رخدادهای محیطی، کارآیی خردحسگرها و سایر عوامل به نمایش می گذارد.
روش DWA مبتنی بر ALO چندهدفه:
الگوریتم بهینه سازی شیر مورچه یک استراتژی بهینه سازی قوی جهت یافتن ماکزیمم و مینیمم در توابع غیرخطی پیوسته می باشد. Gbest در ALO پاسخ موقعیت مورچه ها با توجه به بهترین موقعیت قبلی هر شیر مورچه و بهترین موقعیت های مورچه ها در هر تکرار است.
در مسائل بهینه سازی چندهدفه اهداف بسیاری لازم است تا بطور همزمان بکار گرفته شود. در روش هایALO چندهدفه وزندار، تمامی توابع هدف بصورت ترکیب وزنی در یک رابطه مورد استفاده قرار می گیرند.
![]()
که wti وزن های غیر منفی به فرم ذیل می باشند:
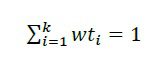
و سپس بهینه سازی مشابه با حالت تک هدفه، برروی F(x) صورت می گیرد.
در روش DWA وزن ها به تدریج عوض می شوند. تغییرات آرام وزن ها بصورت زیر نشان داده می شود:
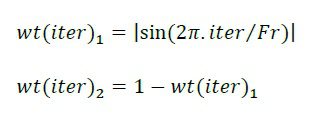
کهiter تعداد تکرار و Fr فرکانس تطبیق می باشد. فرکانس نباید تا حد زیادی بالا و یا پایین باشد تا الگوریتم بتواند در مینیمم همگرا شود. شایسته است که وزن در طی بهینه سازی دوبار از 0 به ۱ تغییر نماید.
پخش بار اقتصادی(economic dispatch):
تجدید ساختار صنعت برق را به شدت رقابتی کرده است که بسیاری از جنبه های صنعت برق را متحول کرده است. در این سناریوی تغییر ، کمبود منابع تجدید پذیر، افزایش قیمت تولید، آلودگی هوا و از همه مهمتر افزایش پیوسته تقاضا برای انرژی برق ، نیاز به پخش بار اقتصادی بهینه را بیش از پیش ضروری کرده است.
موضوع بهره برداری اقتصادی برای یک سیستم قدرت، از نظر برگشت سود سرمایه گذاری انجام شده و اهمیت صرفه جویی در سوخت بسیار مهم است و شرکت های برق تمام تلاش خود را برای به حداکثر رساندن بازدهی ممکن و کاهش هزینه ها انجام می دهند.
پخش بار اقتصادی برای هر شرایط بار پیش بینی شده، توان خروجی هر نیروگاه و نیز هر واحد مولد در داخل یک نیروگاه را تعیین می کند، بطوری که هزینه کلی سوخت مورد نیاز برای تامین بار سیستم را حداقل می کند.
تعریف پخش بار اقتصادی به عنوان یک مسأله بهینه سازی:
مسأله پخش بار اقتصادی در واقع یک مسأله بهینه سازی است که دارای دو بخش تابع هدف و محدودیتها می باشد. تابع هدف در مسأله پخش بار اقتصادی تابع هزینه تولید واحد های نیروگاهی است که به صورت یک تابع درجه دوم در نظر گرفته می شود که از مجموع توابع هزینه همه واحد های نیروگاهی بدست می آید که فقط یک تابع درجه دوم نمی باشد بلکه یک منحني غير محدب است. بخش دوم تعریف محدودیت های مسأله بهینه سازی است، در مسأله پخش بار اقتصادی محدودیت های زیادی وجود دارد از جمله توازن تولید و مصرف در سیستم، زون های ممنوعه ، حدود تولید و نرخ های افزایشی و کاهشی ژنراتور ها و … هستند.
پخش بار اقتصادی یکی از مسائل مهم در بهره برداری از سیستم های قدرت است که در مراکز کنترل انرژی به منظور تعیین خروجی بهینه واحدهای تولیدی استفاده می شود. هدف از حل اینگونه مسائل بهینه سازی، کمينه
کردن هزینه تولید توان و در نتیجه بالا بردن سود سرمایه گذاری است . پخش بار اقتصادی از دسته مسائل بهینه سازی غیرخلی است که شامل قیدهای متعددی از جمله تعادل توان تولیدی و مصرفی، حدود بالا و پایین توان تولیدی ژنراتورها، نرخ شیب تغییرات توان و نواحی ممنوعه تولید است.
پخش بار اقتصادی و روش های حل آن:
هدف از توزیع اقتصادی بار تخصيص تقاضا بين واحدهای مشارکت کننده و از پیش تعیین شده با شرط حداقل نمودن هزینه سوخت و تأمین ذخیره چرخان می باشد. بهره برداری اقتصادی برای یک سیستم قدرت، از نظر برگشت سود سرمایه گذاری انجام شده بسیار مهم بوده و نرخ های تعیین شده به وسیله ارگان های دولتی و اهمیت صرفه جویی در سوخت، شرکت های برق را جهت حصول حداکثر بازدهی ممکن، تحت فشار قرار میدهد. توزیع اقتصادی بار برای هر شرایط بار پیش بینی شده، توان خروجی هر نیروگاه و نیز هر واحد مولد در داخل یک نیروگاه را تعیین می کند، بطوری که هزینه کلی سوخت مورد نیاز برای تامین بار سیستم را حداقل نماید.
پخش بار اقتصادی باید به گونه ای انجام شود که سایر محدودیت های حاکم بر میزان تولید را نیز بر آورده نماید. با بزرگ شدن سیستم قدرت پخش بار اقتصادی نیز پیچیده تر می شود، در نتیجه به دلیل وجود نقاط بهينه محلی زیادیافتن پخش بار بهینه عمومی مشکل تر خواهد شد.
فرمول مسئله:
توزیع اقتصادی بار، روشی با بیشترین کارآمدی، کمترین هزینه بهره برداری یک سیستم قدرت را به وسیله پخش مناسب منابع تولید انرژی برای تأمین بار سیستم تعیین می کند. هدف اولیه آن به حداقل رساندن هزینه کل تولید با در نظر گرفتن محدودیت های بهره برداری منابع تولید وژنراتوری می باشد. مسأله توزیع اقتصادی بار، مقدار بار را برای نیروگاه ها به منظور کم کردن هزینه ها معین می کند. فرمول بندی آن نیز به عنوان یک مسأله بهینه سازی برای به حداقل رساندن هزینه کلی سوخت مجموع نیروگاه هایی که بار و تلفات را تأمین می کنند ارائه می شود . بنابر این مسأله توزيع اقتصادی بار می تواند با تابع هدف زیر بیان شود.
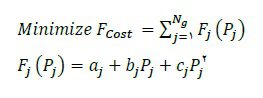
محدودیت های مساوی و نامساوی:
هر مسئله بهینه سازی دارای محدودیت ها و قید هایی است که این قید ها و محدودیت ها برای پخش بار اقتصادی بیان شده است.
توازن تولید و مصرف در سیستم:
لازم است در هر لحظه از فعالیت سیستم قدر است، مجموع توان مصرفی و تلفات برابر با توان تولید شده توسط ژنراتورها بأشد.
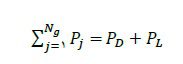
که در آن PD توان مورد تقاضا و PL تلفات سیستم است. تلفات سیستم تابعی از توان تولیدی ژنراتورها است که مقدار آن با استفاده از رابطه زیر قابل محاسبه است:
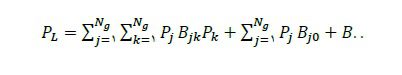
که در آن Bjk و Bj0 و …B ضرايب تابع تلفات شبکه مستند.
حد بالا و پایین توان تولیدی ژنراتورها:
در هر لحظه از فعالیت سیستم قدرت توان تولیدی هر واحد تولیدی نباید از حد بالا و پایین آن تجاوز کند، این محدودیت با نامساوی زیر بیان می شود:
![]()
که در آن Pjmax و Pjmin به ترتیب حد بالا و پایین توان تولیدی ژنراتور j ام است.
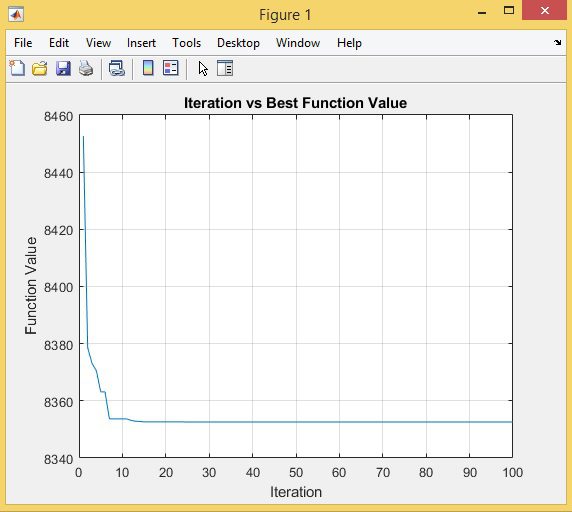
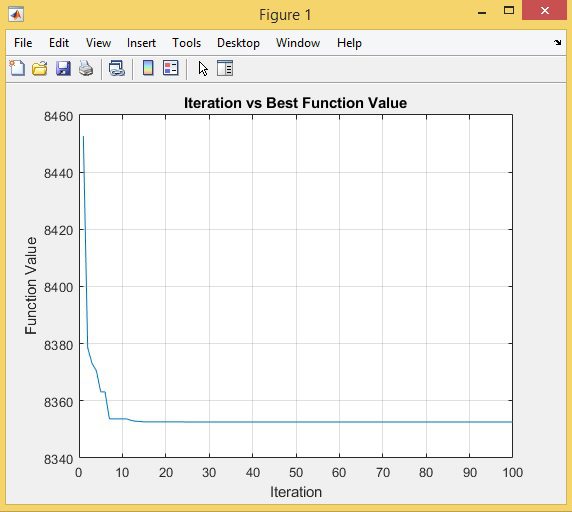
نتایج الگوریتم بهینه سازی شیرمورچه چندهدفه برای حل مسئله پخش بار اقتصادی