توضیحات
حل معادله دیفرانسیلی مرتبه دوم غیرخطی نوسان ساز ون در پل(Van der Pol) با روش ode45 در نرم افزار متلب(MATLAB) و سیمولینک(SIMULINK)
شرح پروژه:
در این پروژه حل معادله دیفرانسیلی مرتبه دوم غیرخطی نوسان ساز ون در پل(Van der Pol) با روش ode45 در نرم افزار متلب(MATLAB) و سیمولینک(SIMULINK) کدنویسی و شبیه سازی شده است. در این پروژه علاوه بر کدهای متلب و سیمولینک گزارش کامل فارسی پروژه را نیز دریافت خواهید کرد.
نوسان ساز ون در پل:
نوسان ساز ون در پل(van der Pol oscillator)، به صورت معادله دیفرانسیلی مرتبه دوم غیرخطی بیان می شود.
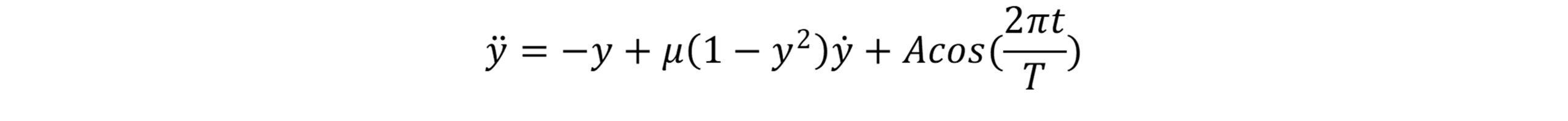
در معادله دیفرانسیلی فوق، y بیانگر موقعیت است که تابعی از زمان t می باشد. μ پارامتر اسکالر است که نشان دهندة غیرخطی بودن و سختی میرایی است. زمانیکه μ برابر صفر باشد، هیچ گونه تابع میرایی وجود ندارد. بنابراین معادله نوسان ساز ون در پل به صورت نوسان ساز هارمونیک ساده در می آید. زمانیکه μ>0 باشد سیستم نوسان ساز وارد یک چرخه حدی(cycle limit) خواهد شد.
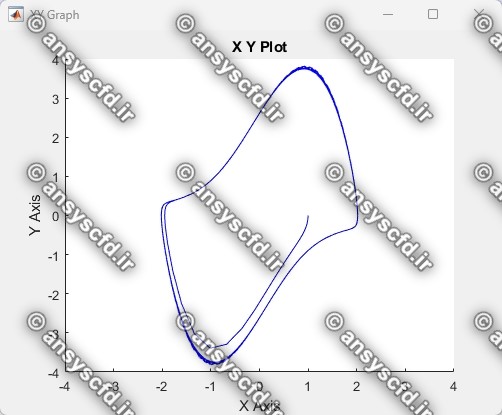
از معادله غیرخطی ون در پل مشاهده می شود که این معادله یک سیستم غیرمحافظه کار را مدلسازی می کند که در آن به مقدار1> |y| انرژی به سیستم افزوده و به مقدار 1< |y| انرژی از سیستم کم می شود. بنابراین یک حرکت تناوبی به نام چرخة حدی پدید می آید که در آن انرژی در دامنه های بالا از بین می رود و در دامنه های پایین تولید می شود. همچنین در پیرامون هر حالت، نوسان هایی پدید می آید که در آن میان تولید و اتلاف انرژی، تعادل برقرار می کند. پدیدة مهم چرخة حدی را با دینامیک نوسان ساز میتوان نشان داد که ون در پل برای نخستین بار در سال 1927 میلادی آن را بررسی کرد و در آزمایش لامپ خلاء به کارگرفت.
از آنجاییکه معادله دیفرانسیلی ون در پل به صورت مرتبه دوم است بایستی برای حل با روش ode45 به دو معادله دیفرانسیلی مرتبه اول تبدیل شود.
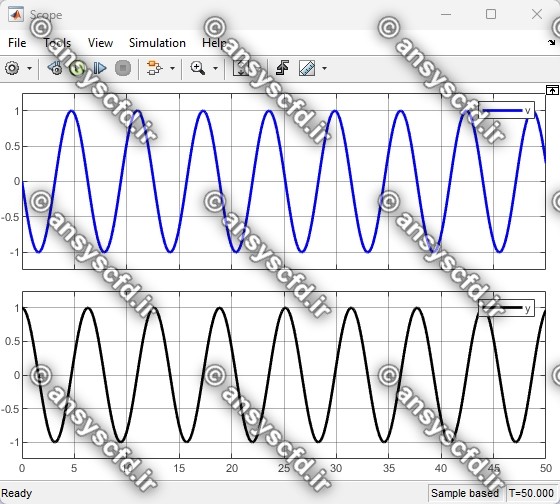
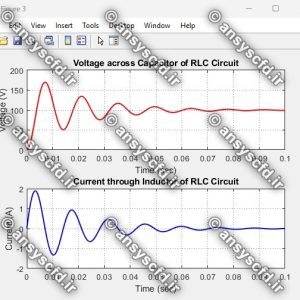
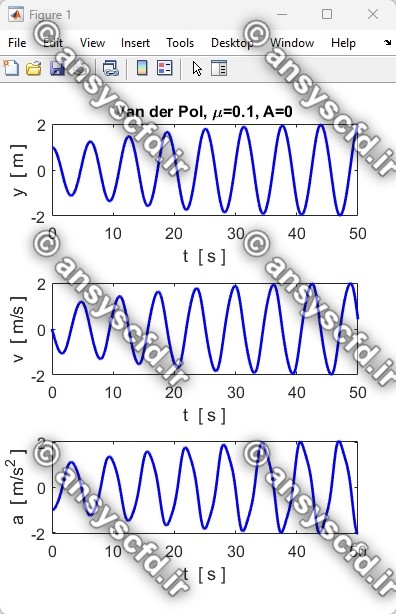
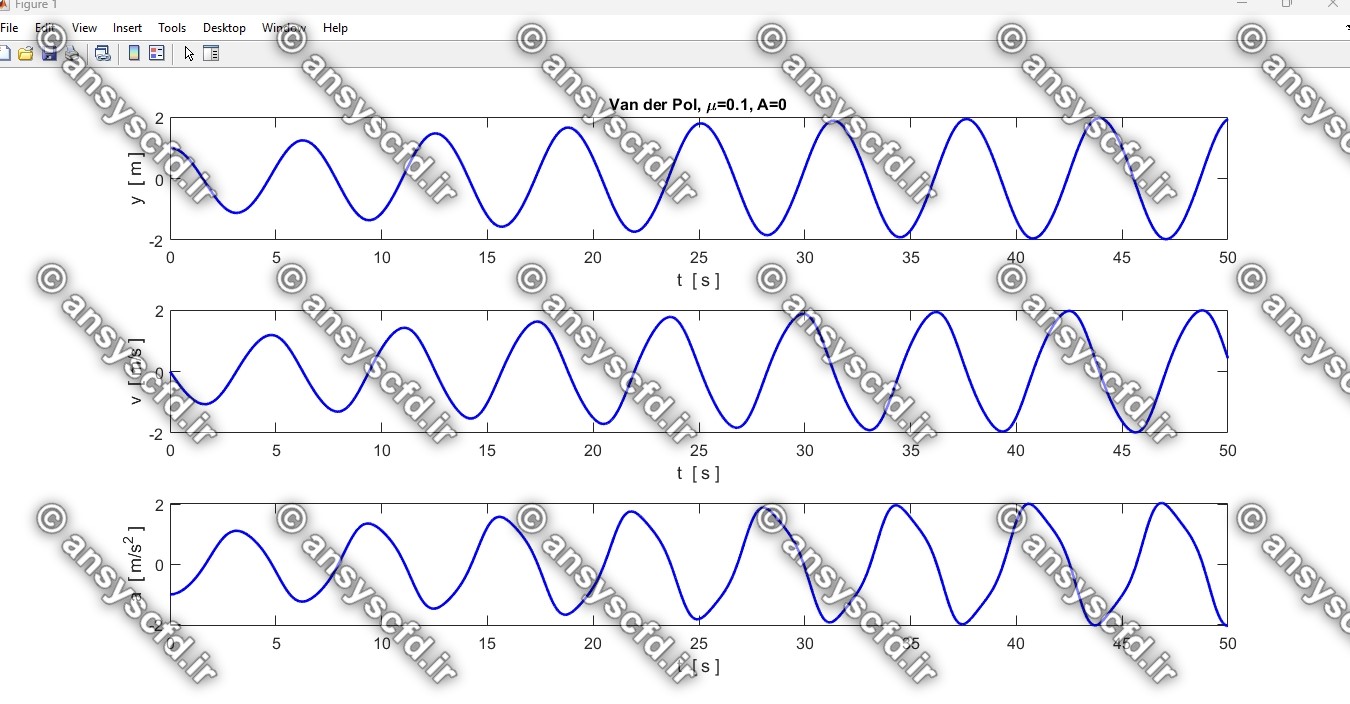
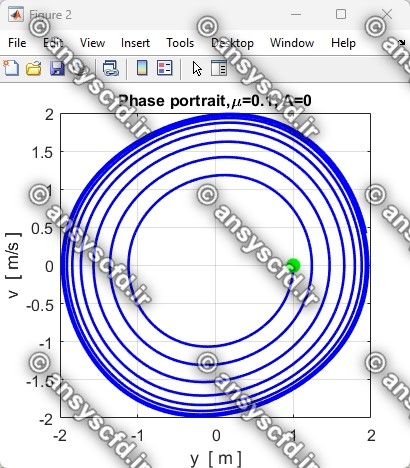
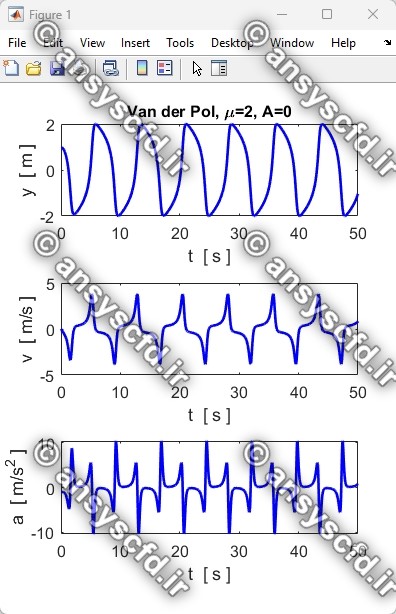
نتایج حل معادله دیفرانسیلی مرتبه دوم غیرخطی نوسان ساز ون در پل(Van der Pol) با روش ode45 در نرم افزار متلب:
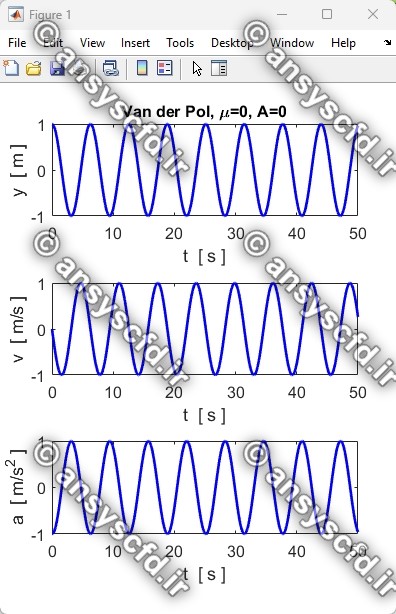
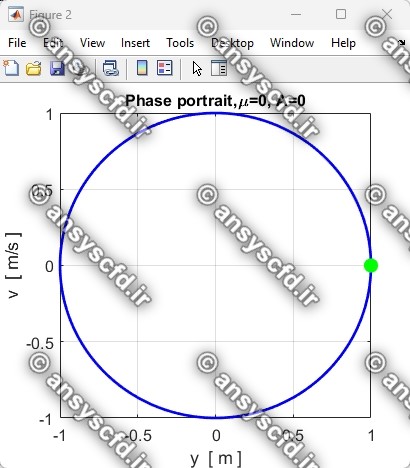
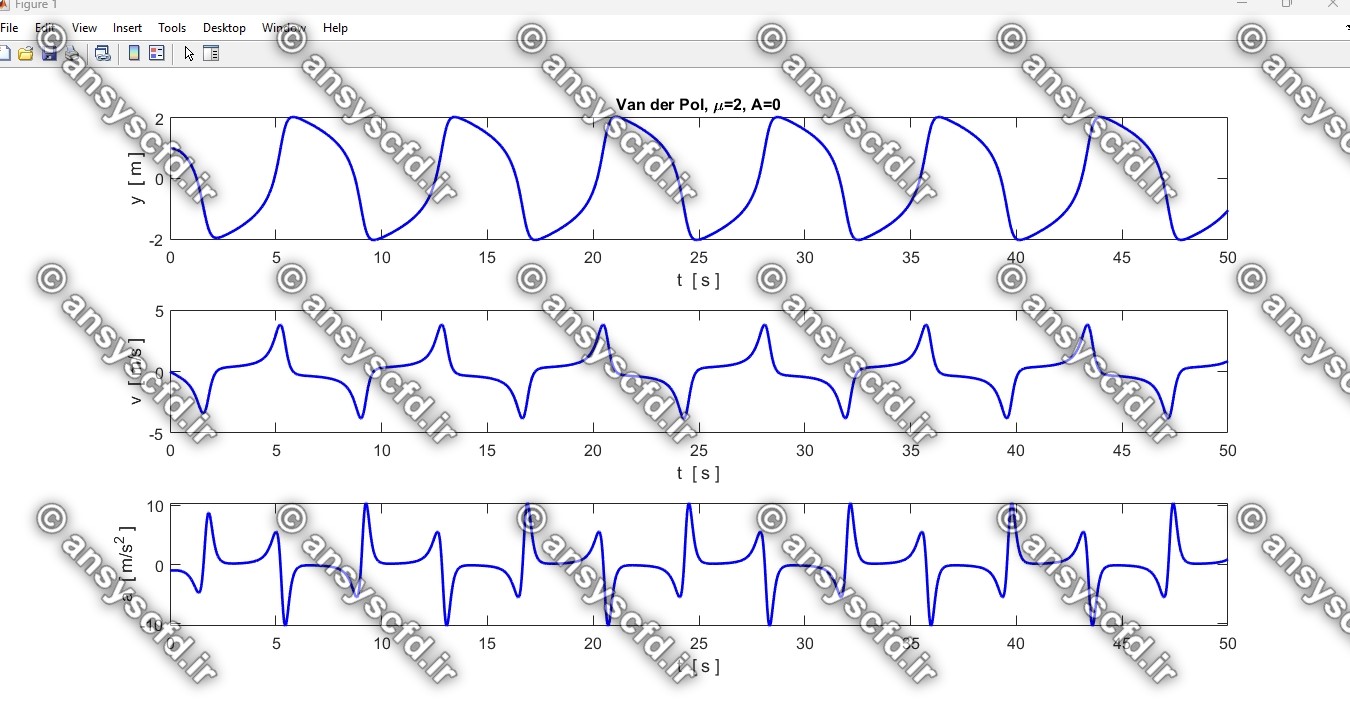
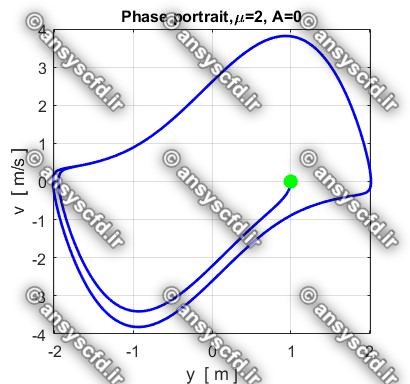
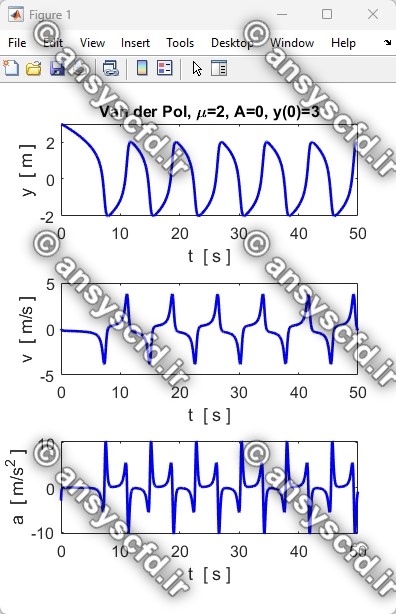
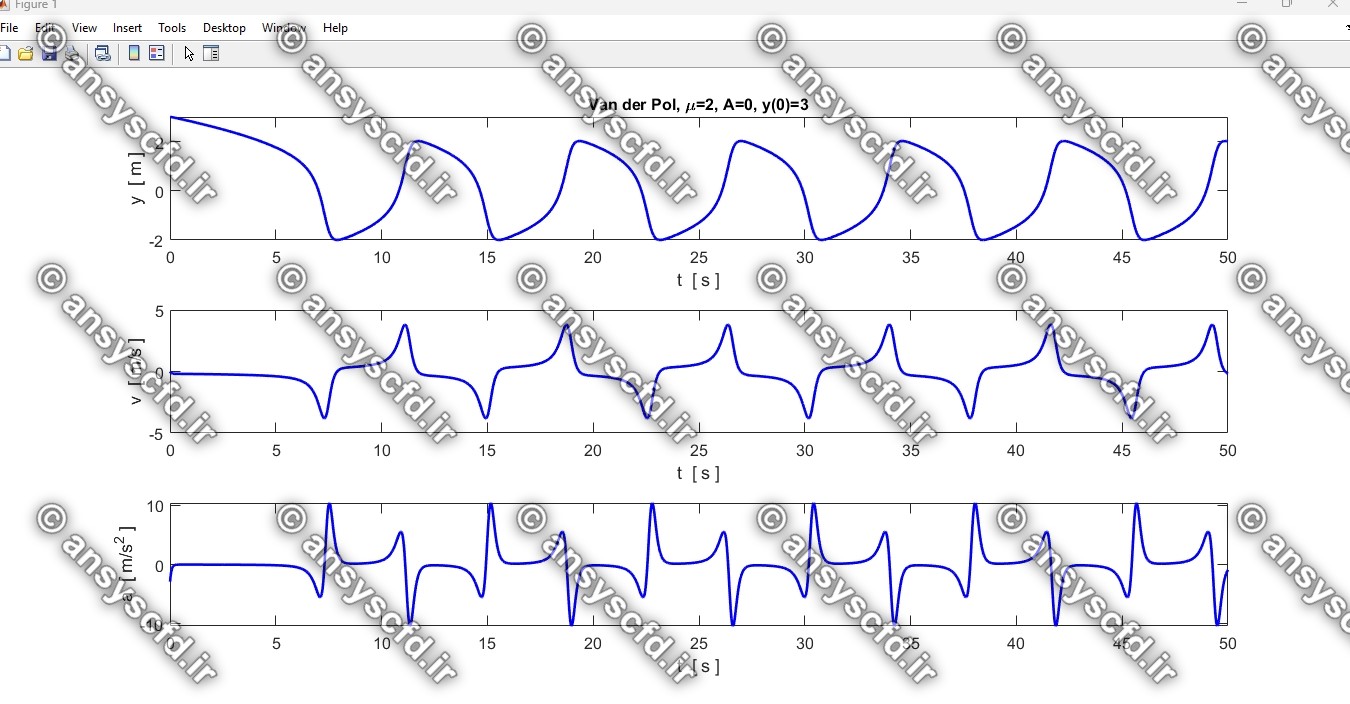
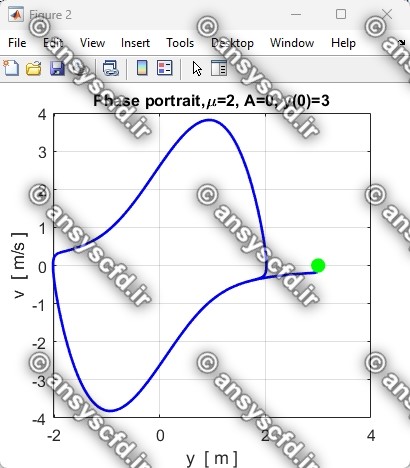
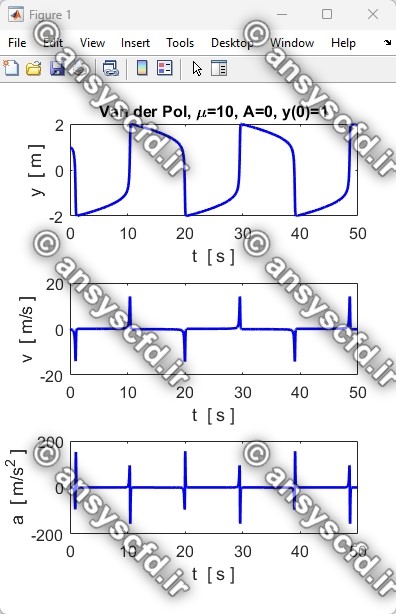
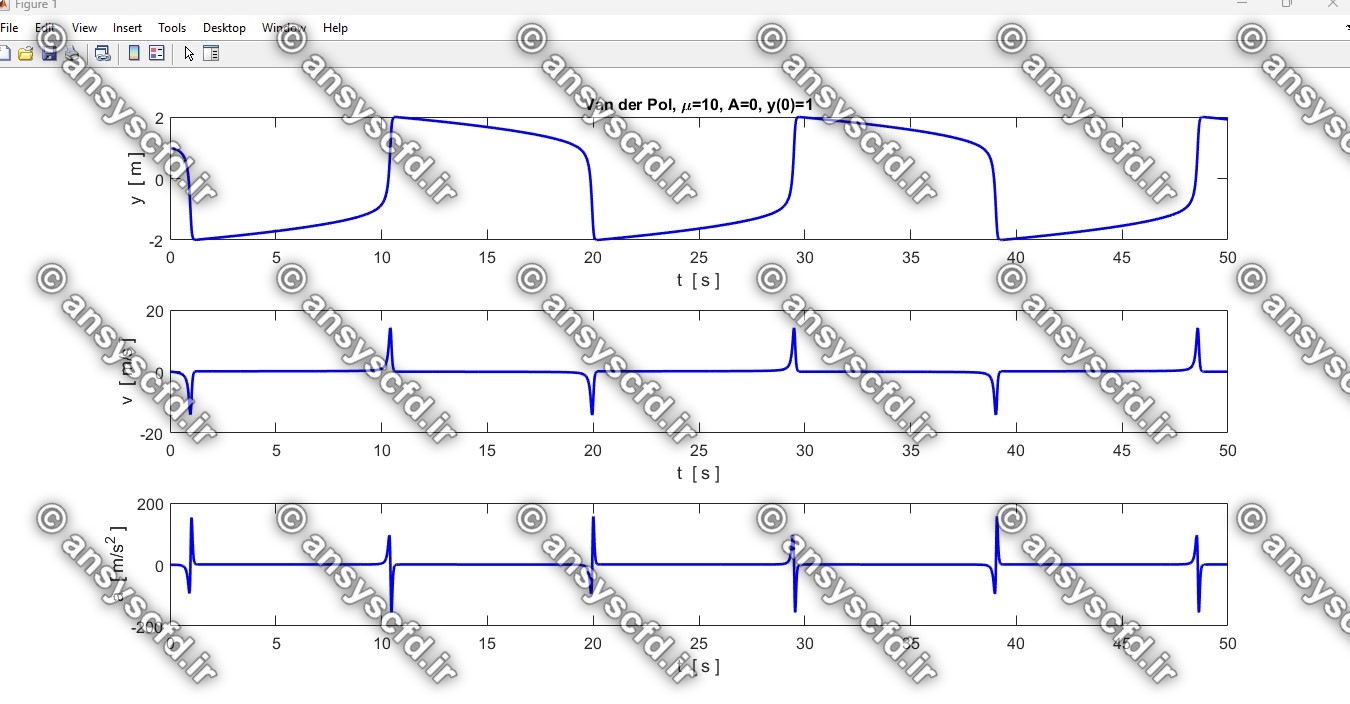
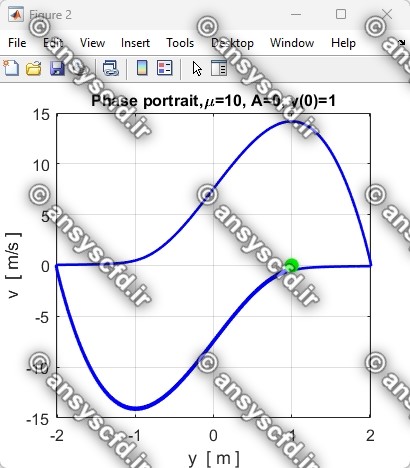
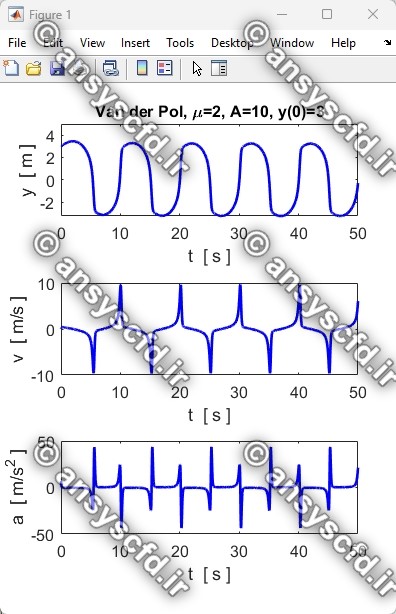
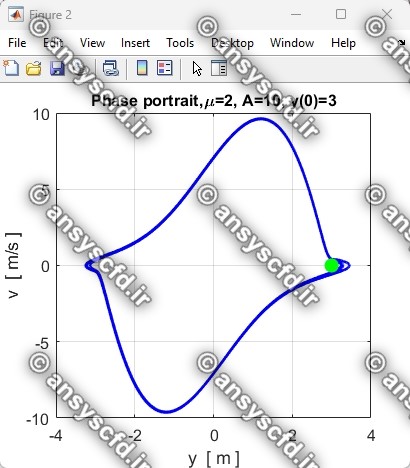
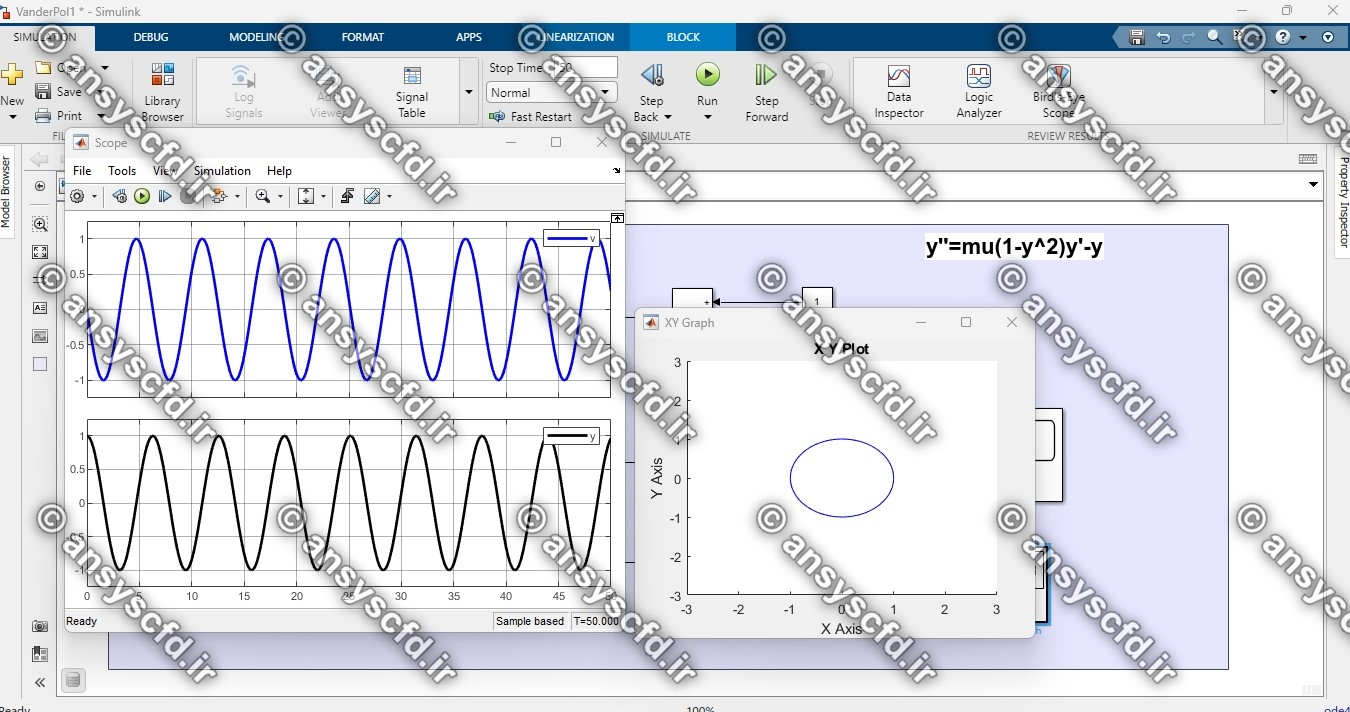
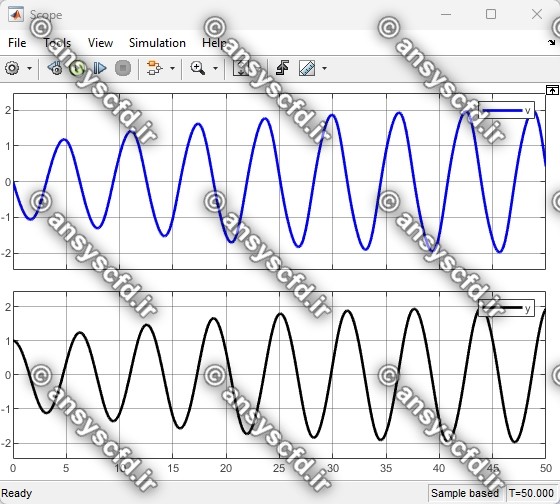
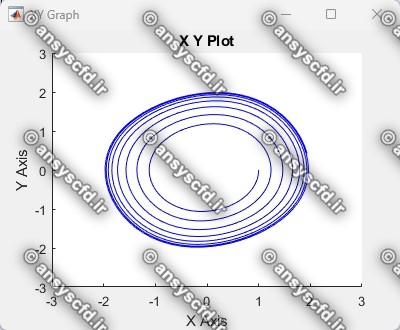
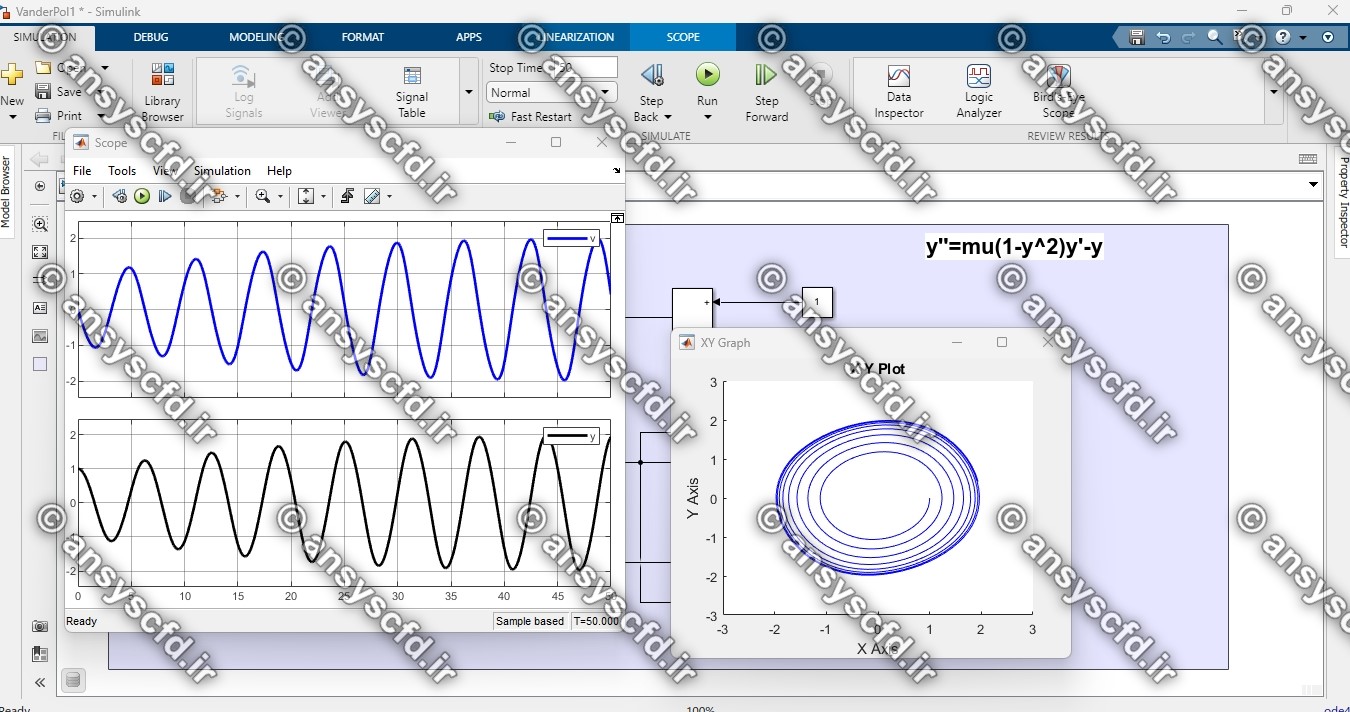
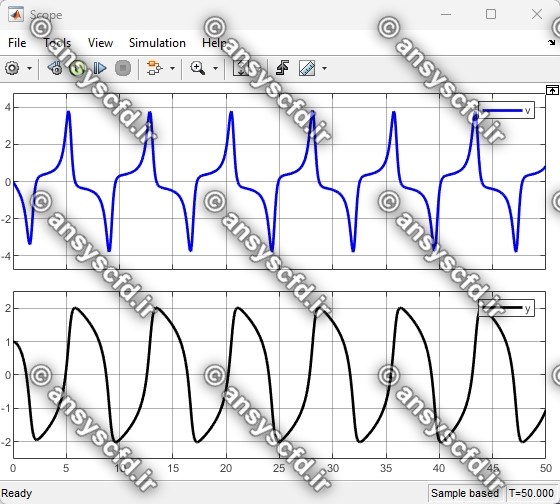
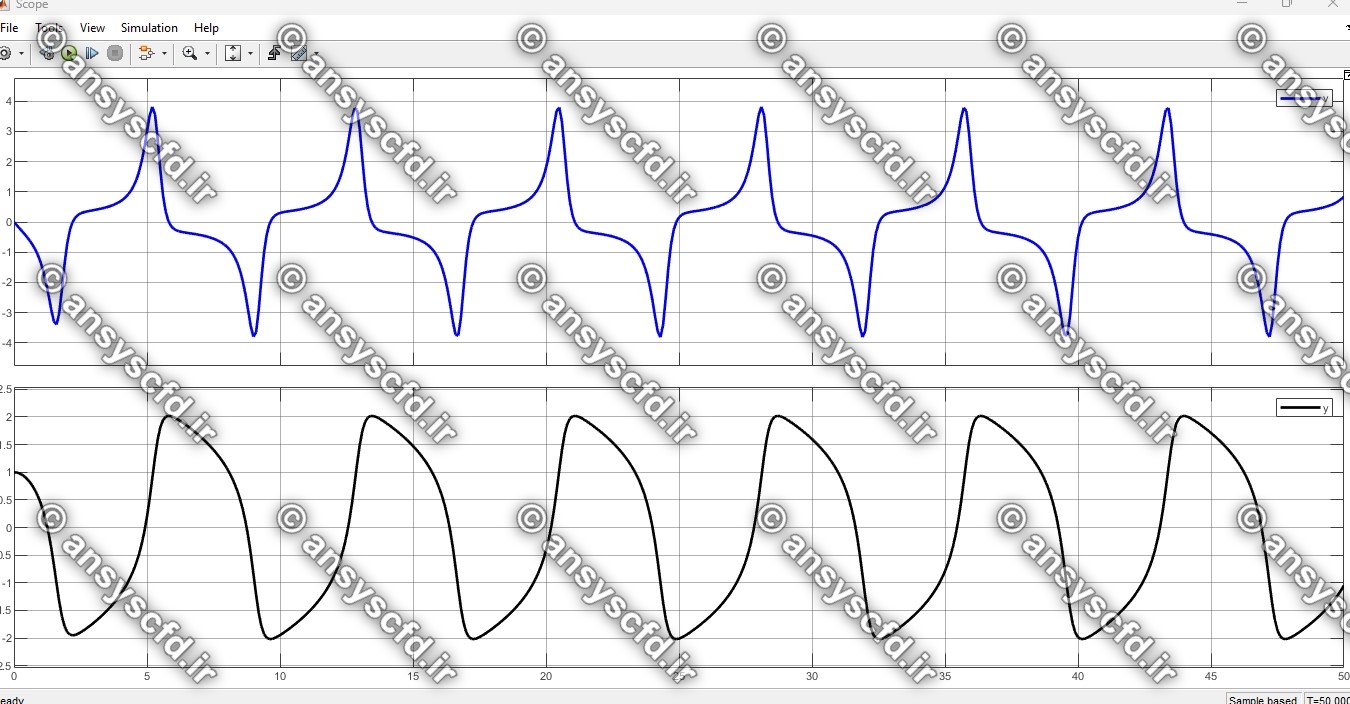
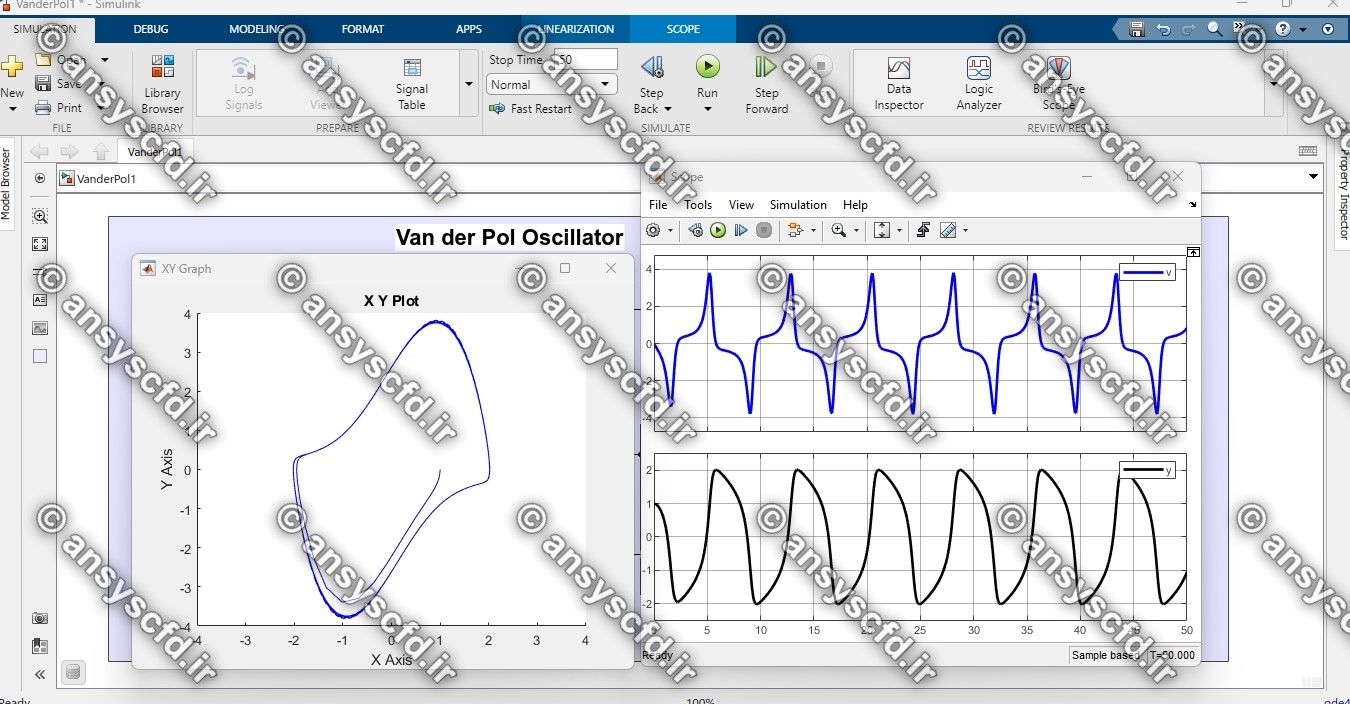
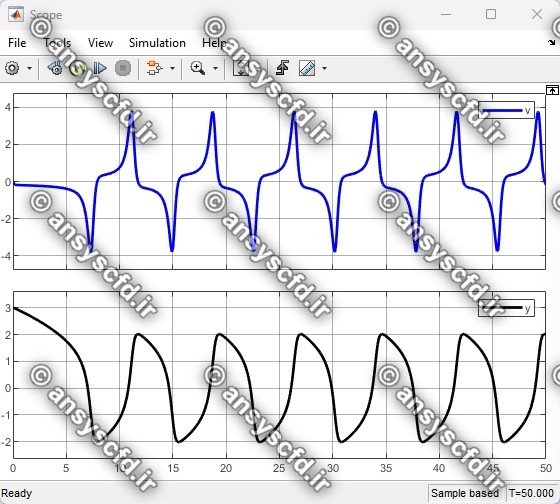
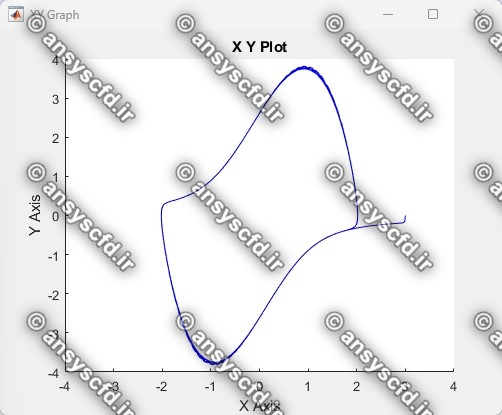
نتایج حل معادله دیفرانسیلی مرتبه دوم ون در پل در سیمولینک متلب: