توضیحات

پروژه متلب جریان در یک کانال دو بعدی با روش شبکه بولتزمن(LBM)

 

دانلود مقاله مرجع

 

روش شبکه بولتزمن:

شبیه سازی و تحلیل جریان سیالات موضوع بسیار مهمی در مبحث دینامیک سیالات محاسباتی محسوب می­شود. باتوجه به نوع سیال، هندسه جریان و رژیم حاکم بر جریان سیالات مدل های گوناگونی برای تحلیل جریان سیالات وجود دارد. یکی از قوی ترین مدل کننده های مطرح در دینامیک سیالات محاسباتی، معادله بولتزمن می باشد که در سال ۱۸۷۲ توسط دانشمند بزرگ اتریشی به نام لودویگ بولتزمن به دست آمد. این معادله قادر است با رویکردی میکروسکوپیک و جنبشی انواع جریان های سیال را شبیه سازی کند. از آنجایی که این معادله از پیچیدگی های خاصی برخوردار است و حل تحلیلی آن غیرممکن و حل عددی آن نیز کار بسیار دشواری است، در حدود سال ۱۹۸۸، مک ناوارا و زانتیا موفق شدند برای اولین بار با ارائه روشی تحت عنوان روش شبکه بولتزمن (LBM)، این معادله را ساده و قابل حل نمایند. با در اختیار داشتن معادله گسسته بولتزمن و بیان الگوریتم حل روش شبکه بولتزمن می توان جریان سیالات را شبیه سازی کرد. در واقع روش شبکه بولتزمن روش بسیار پر قدرتی است که می تواند با حل معادله ی آماری بولتزمن و طی کردن مسیری کاملا مستقل از معادله ی ناویر استوکس تأثیر بسزایی در علم مکانیک سیالات داشته باشد. با توجه به ویژگی های منحصر به فرد این روش، نظیر داشتن کدهایی ساده و سریع با هسته های محاسباتی مستقل، قابلیت اجرای موازی و بکارگیری هم زمان چندین حافظه ی کامپیوتری، شرایط مرزی مناسب و متنوع و با اجرای بسیار ساده، عملکرد در محدوده وسیعی از رژیم های سیال و غیره، این روش را در جایگاه بسیار بالایی در دنیای مکانیک سیالات محاسباتی قرار داده است.

روش های تحلیل جریان سیالات:

برای شبیه سازی و تحلیل جریان سیالات، مدل ها یا معادله های مختلفی وجود دارد که هر یک در محدوده ای از رژیم سیال حاکم می باشند. رژیم سیال توسط پارامتر بی بعدی به نام عدد نادسن (Knudsen number) مشخص می شود که برابر با نسبت طول آزاد میانگین مولکولی به مقیاس طولی مشخصه جریان است.

در بین مدل کننده های مطرح می توان معادلات ناوير-استوکس، اویلر، بورنت ( Brunette) و معادله بولتزمن را نام برد. در حالیکه معادله ناویر استوکس فقط در محدوده رژیم پیوسته و لغزشی، معادله اویلر فقط در محدوده رژیم پیوسته و معادلات بورنت تنها در محدوده ی رژیم گذرا برقرار است. معادله بولتزمن در سرتاسر این محدوده حاکم است. شكل زیر ارتباط میان رژیم سیال و عدد نادسن را نمایش می دهد.

شکل نحوه تغییرات رژیم سیال در محدوده تغییرات عدد نادسن(Kn).

 

روش های حل تحلیلی:

اولین روشی که برای حل هر مسئله ای به ذهن می رسد، حل تحلیلی معادلات حاکم بر آن است. اما برای تعداد بسیار کمی از جریان ها حل تحلیلی موجود است. تقریباً تمام مسائل مهم مهندسی فاقد حل تحلیلی است. لذا همگام با پیشرفت تکنولوژی و توسعه کامپیوترها، روش های حل عددی معادلات حاکم بر جریان سیال مورد توجه قرار گرفته اند.

روش های عددی مرسوم:

روش های اختلاف محدود، حجم محدود و اجزای محدود از جمله ی روش های متداول عددی هستند که از طریق گسسته سازی، جبری سازی، خطی سازی و حل دستگاه معادلات، جریان را تحلیل می کنند. باید توجه کرد که در این روش ها معادلات ناویر استوکس به عنوان معادلات حاکم بر جریان در نظر گرفته شده و با حل آنها جریان تحلیل می شود. باید توجه داشت که این معادلات تنها بر رژیم جریان پیوسته حاکم هستند. در برخی جریان ها مانند جریان در میکرو کانال ها، اندازه طول آزاد میانگین مولکولی در مرتبه مقیاس طولی مشخصه جریان است و دیگر نمی توان جریان را پیوسته فرض کرد و اصطلاحا جریان رقیق است. برای حل این نوع جریان ها دیگر نمی توان از روش های حل عددی معادلات ناویر استوکس بهره برد.

روش های شبیه سازی برخوردهای مولکولی:

در این روش ها برخوردهای بین مولکولی شبیه سازی می شوند و از این طریق، مشخصات جریان در سطوح میکروسکوپی و ماکروسکوپی حاصل می گردد. مشکل عمده این روش ها این است که برای بازسازی حتی یک لحظه کوچک از حرکت سیال، حجم محاسبات بسیار زیاد بوده و امکانات عظیم کامپیوتری مورد نیاز است. این مشکلات باعث می شود که برخوردهای مولکولی از دیدگاه آماری به عنوان روش مناسب تر در نظر گرفته شود.

روش های مبنا ذره ای:

یکی از روش های مبنا ذره ای برای شبیه سازی جریان های با عدد نادسن بالا، شبیه سازی مستقیم مونت کارلو است. این روش برخورد ذراتی را شبیه سازی می کند که خود این ذرات نماینده گروهی از مولکول ها هستند که خواص یکسانی نظیر سرعت و دما دارند. بنابراین نیازی به در نظر گرفتن تک تک مولکول ها در میدان حل نیست.

روش های شبکه ای:

در سال ۱۹۸۶، فریش، هاسلاچر و پومئو موضوعی شگفت انگیز را بیان کردند. ایجاد یک ماشین سلولی ساده که فقط از قوانین بقاء در سطح میکروسکوپی پیروی می کند و قادر به بازسازی پیچیدگی جریان های سیال واقعی است. به دنبال این کشف در بحث دینامیک سیالات تحولی بزرگ ایجاد شد و به ایجاد روش های جدید شبکه گاز(LGM یا Lattice Gas Method ) و شبکه بولتزمن(LBM) برای تحلیل جریان انجامید. در این روش ها برخورد ذرات مجازی که بر روی یک شبکه منظم قرار گرفته اند بررسی می شود. تفاوت آن با روش مبنا ذره ای این است که در آنجا ذره می توانست در هر جهت حرکت کند ولی در روش شبکه این ذرات مجازند فقط بر روی مسیرهای مشخصی حرکت کنند. نوع ذرات و قواعد برخورد در سطح میکروسکوپی منطبق بر واقعیت فیزیکی نیست ولی الگوریتم های آنها در سطح ماکروسکوپی منجر به ارضای معادلات بقای جرم و مومنتم می گردد.

صریح بودن کلیه محاسبات، قابلیت پردازش موازی و سهولت استفاده از آن در مسائل با هندسه پیچیده مورد توجه اند. در شکل زیر محدوده مناسب برای استفاده از هر یک از روش های ذکر شده، نشان داده شده است. مشاهده می شود که روش های عددی که معادلات ناویر استوکس بر آنها حاکم است در محدوده ای که عدد نادسن کوچک است کارایی دارد و برای سیستم های با ابعاد کوچکتر، با بزرگتر شدن عدد نادسن به ترتیب روش های شبکه ای (روش شبکه گاز و روش شبکه بولتزمن)، روش های مبنا ذره ای و روش دینامیک مولکولی مناسب است.

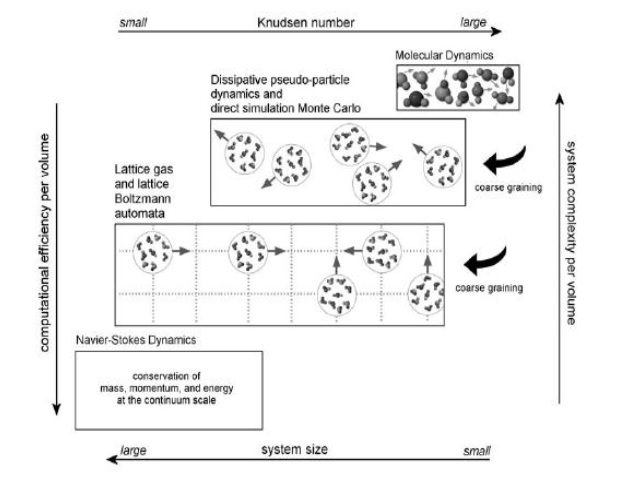
شکل نمایی از شرایط مناسب برای استفاده از روش های مختلف تحلیل جریان.

 

روش شبکه بولتزمن:

برای بررسی وضعیت دینامیکی هر سیستم از دیدگاه آماری، فضایی سه مولفه ای به صورت(x,p,t) تحت عنوان فضای فازی و یا فضای سرعت تعریف می گردد که در آن x بیانگر موقعیت ذرات نسبت به مبدا مشخص، p بیانگر اندازه حرکت ذرات و t نیز نشان دهنده زمان است. برای توصیف دقیق وضعیت دینامیکی هر سیستم در این فضا،                          تابع f^(N) (x^(N), p^(N), t^(N)) با نام تابع توزيع تعریف می شود که در آنN معرف تعداد ذرات و f بیانگر وجود این تعداد ذره در لحظه t، در مکان x و با اندازه حرکت p است. همواره برای هر سیستم گاز N عددی از مرتبه عدد آووگادرو است. لذا چنین توصیف دقیقی توسط تابع توزیع f^(N) از وضعیت دینامیکی سیستم گاز و حل و تحلیل معادلات دینامیکی برای تک تک ذرات در هر نوع کامپیوتر عملا امکان ناپذیر است. اما خوشبختانه با استفاده از تابع توزیع تک ذره ای ⁽¹⁾f هم می توان به پاسخ هایی با دقت بسیار مناسب دست یافت. f⁽¹⁾ (x,p,t) بیانگر احتمال حضور یک ذره در لحظه ای در مکانx و  و با اندازه حرکت p است. با استفاده از تابع توزیع تک ذره ای، معادله جنبشی گازها به صورت ذیل است.

این معادله نشان دهنده نحوة تغییرات تابع توزیع در فضای فازی تعریف شده برای محیط سیال است. سمت چپ عملگر جریان نام دارد و بیانگر حرکت و جریان ذرات در مسیرهای تأثیرپذیر از میدان نیرویی F و سمت راست آن C₁₂ دربرگیرنده اثرات برخورد میان ذرات سیال است که منجر به ورود مولکول ها به و یا خروج آنها از مسیرهای گفته شده می گردد.

C12 عملگر برخورد نامیده می شود و به تابع توزیع دو ذره ای وابسته است. اگر معادله جنبشی بر حسب تابع توزیع دو ذره ای f₁₂ نوشته شود در آن صورت عملگر برخورد معادله جدید به دست آمده به تابع توزیع سه ذرهای وابسته خواهد بود که آن نیز منجر به رسیدن به تابع توزیع چهار ذره ای شده و این روند تا N ذره ادامه دارد. بولتزمن با چندین فرض ساده دقیق به این رشته بی انتها که به سلسله مراتب شهرت دارد خاتمه داد و عملگر برخورد در معادله جنبشی را به صورت ذیل ارائه داد.

1و2 معرف جهات حرکت دو ذره قبل از برخورد و 2’ ، 1’ نشان دهنده جهات حرکت ذرات پس از فرایند برخورد است. با جایگذاری این عبارت در معادله جنبشی، معادله معروف بولتزمن به صورت ذیل حاصل می شود.

همانطور که دیده می شود، علیرغم ساده سازی های بولتزمن و اینکه معادله جنبشی تنها برحسب تابع توزیع تک ذره ای نوشته شده بود، باز هم معادله به دست آمده یک معادله دیفرانسیلی – انتگرالی پیچیده است که حل تحلیلی آن غیرممکن و حل عددی آن کار بسیار دشواری است.

در سال های اخیر، روش شبکه بولتزمن یا لتیس بولتزمن(LBM) به عنوان یک طرح عددی مطلوب برای شبیه سازی جریان های سیال و مدلسازی فیزیک سیالات، توسعه یافته است. ایده اساسی لتیس بولتزمن ساختن مدل هایی از فرایندهای میکروسکوپی است که خواص ماکروسکوپی حاصل از این مدل ها از معادلات ماکروسکوپی مورد نظر تبعیت کنند. فرض بنیادی برای استفاده از این روش های ساده شده جنبشی برای جریان های ماکروسکوپی سیال این است که دینامیک ماکروسکوپی سیال نتیجه رفتار جمعی ذرات میکروسکوپی در سیستم است و تمرکز اصلی لتیس بولتزمن(LBM) بر روی رفتار ماکروسکوپی متوسط است.

روش شبکه بولتزمن توسط تابع توزیع تک ذره ای(f_i) (Distribution function) که عددی حقیقی است بیان می شود. درواقع به جای دنبال کردن یک ذره منفرد، با تاریخچه زمانی یک جمعیت گروهی سر و کار داریم، که احتمال حضور آن را به صورت یک ابر میکروسکوپی می توان تجسم نمود(شکل زیر).

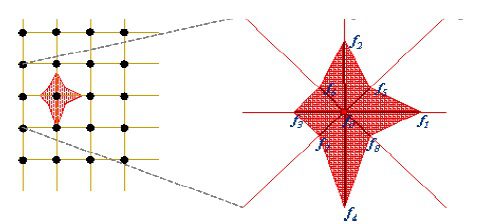
شکل  نمایش ابر میکروسکوپی تابع توزیع ذره.

 

در روش شبکه بولتزمن ذرات مجازی در روی یک شبکه منظم برخورد داده می شوند ولی به جای مشخص نمودن آرایش ذرات مجازی احتمال حضور این ذرات در مسیرهای مختلف معرفی و مورد استفاده قرار می گیرد. این احتمال با f_i نمایش داده می شود. تجدید آرایش ذرات طی مراحل برخورد و جاری شدن رخ می دهد و از معادلة بولتزمن برای محاسبة توابع توزيع جديد استفاده می گردد. مدل های مختلف حرکت و برخورد ذرات در شبکه بولتزمن در حالت عمومی به صورت D_mQ_n نامگذاری می­شود که m بیانگر بعد و n بیان کننده تعداد جهاتی است که برای حرکت ذرات سیال در هر نقطه از شبکه در نظر گرفته شده است. به عنوان نمونه هایی از شبکه ها می توان، شبکه های D1Q3 ،D1Q5  و D2Q9 را نام برد.(اشکال زیر).

شکل سمت راست شبکه بولتزمن D3Q15 و شکل سمت چپ شبکه بولتزمن D3Q19.

 

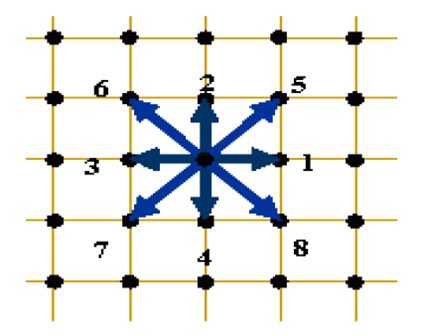
شکل شبکه بولتزمن D2Q9.

 

ملاحظه می شود که در شبکه هر گره می تواند از هشت مسیر مختلف با گره های مجاورش ارتباط برقرار کند. احتمال حضور ذره در مرکز هر گره با f₀ نشان داده می شود. در مدل دو بعدی D2Q9 در هر یک از نقاط شبکه 9 جهت حرکت برای ذرات سیال به سمت سایر نقاط وجود دارد. بنابراین در هر یک از نقاط این مدل 9 مقدار برای تابع توزيع f تعریف می شود که هریک نشان دهنده چگالی ذرات سیال در جهت مربوط به خود هستند. روابطی که کمیت های ماکروسکوپی سیال (p چگالی و u سرعت)  را در هر یک از نقاط شبکه به f_i  (پارامتر میکروسکوپیک شبکه) مرتبط می کنند عبارتند از :

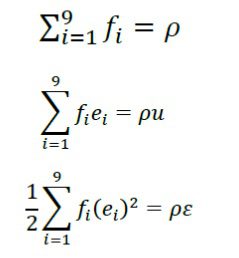
به عبارت دیگر تابع توزیع به گونه ای تعریف می شود که منجر به ارضای معادلات بقای جرم، مومنتم و انرژی گردد. E_i بیانگر جهات سرعت شبکه در مسیرهای شبکه است.

گسسته سازی معادله بولتزمن:

مک نامارا و زانتی توانستند با محدود کردن هر سه پارامتر فضای فازي(x,p,t) به مقادیر مشخص، معادله بولتزمن را به شدت ساده و قابل حل نمایند. آنها با انطباق یک شبکه تحت عنوان شبکه بولتزمن به ناحیه حل جریان سیال، بینهایت مکان ممکن برای قرارگیری ذرات سیال را به نقاط شبکه محدود نمودند.

سپس با محدود کردن جهت حرکت ذرات سیال هنگام جاری شدن از یک نقطه به سمت سایر نقاط، بردار سرعت و متعاقب آن بردار اندازه حرکت سیال را نیز از حالت پیوسته خارج نموده و نهایتا با گسسته سازی زمان به بازه هایی مشخص هر سه پارامتر فضای فازی يعنی x,p,t  را از حالت نامحدود و بینهایت مقداری به حالتی کاملاً گسسته و تحت شبکه تبدیل نمودند.

یکی از پارامترهای بسیار تأثیرگذار در پاسخ روش شبکه بولتزمن، پارامتر زمان آسودگیt است. این پارامتر معیاری از زمان به تعادل رسیدن ذرات سیال در هر یک ازn  جهت مفروض برای حرکت ذرات سیال است.

زمان آسودگی که ابزاری برای برقراری سازگاری میان روش شبکه بولتزمن و معادله بولتزمن است، مطابق رابطه زیر به طور مستقیم در مقدار لزجت سینماتیک سیال تأثیر گذار است.

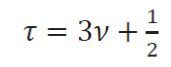
در روش شبکه بولتزمن بر اساس انتخاب مقدار t، معادله بولتزمن توسط یکی از دو روش زمان آسودگی منفرد (SRT) (Single- time relaxation) و زمان آسودگی چندگانه(MRT) (Multi- relaxation- time) ساده و قابل حل می­شود. در روش زمان آسودگی منفرد، زمان به تعادل رسیدن ذرات در تمام n جهت یکسان فرض می شود اما در روش زمان آسودگی چندگانه در هر یک از n جهت مقدار ویژه ای برای t منظور می گردد. این روش نسبت به روش زمان آسودگی منفرد دقیق تر و زمان اجرای کدهای آن نیز طولانی تر است. با به کارگیری روش SRT و مدل D2Q9 معادله بولتزمن به صورت زیر در می آید که به معادله گسسته بولتزمن معروف است.

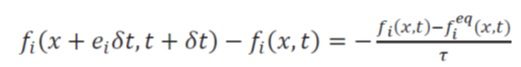
f_i^eq بیانگر تابع توزیع تعادلی با چگالی ویژه جهتی در جهت i، پس از برقراری تعادل در این جهت است که به صورت زیر تعریف می گردد:

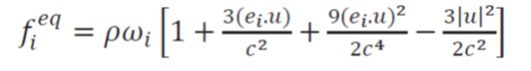
 در معادله، C سرعت صوت و w ضرایب وزنی می باشند که با استفاده از تقريب عدد ماخ کوچک به دست می آیند. مؤلفه های سرعت شبکه در مسیرهای مختلف به صورت زیر بیان می شوند.

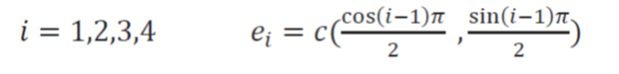
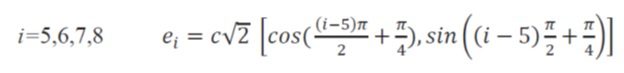
سرعت های شبکه باتوجه به شکل شبکه(طول هر مسير) و با توجه به اینکه مدت زمان رسیدن به گره همسایه در تمام مسیرهای یکسان و بر ابر گام زمانی شبکه است، تعیین می شود.

ویژگی های روش شبکه بولتزمن (مزایا و معایب):

• ساده سازی و قابل حل نمودن معادله پیچیده بولتزمن توسط این روش
• الگوریتم حل در روش شبکه بولتزمن به گونه ای می باشد که برای کد نویسی آن به دستورات بسیار ساده ای نیاز است.
• قابلیت اجرای موازی کد نوشته شده توسط LBM توسط چندین حافظه مختلف به دلیل ایجاد هسته های محاسباتی مستقل در کدهای نوشته شده.
• بالاتر بودن سرعت کدهای نوشته شده توسط روش شبکه بولتزمن نسبت به روش هایی نظیر تفاضل محدود برای حل معادلات ناویر استوکس در موارد مشابه.
• مدلسازی شرایط مرزی پیچیده، دینامیک فصل مشترک جریان های چند فاز و جریان های مغشوش
• ضعف در مدلسازی جریان های چند فازی گاز – مایع با اختلاف چگالی و یا اختلاف گرانروی زیاد بین فازها
• ضعف در شبیه سازی جریان هایی با اعداد ماخ بالا.

شرط های مرزی:

دو دسته شرط مرزی رایج در دینامیک سیالات محاسباتی وجود دارد. مرزهای باز و مرز دیوار جامد. در حالت کلی در روش شبکه بولتزمن دو راه برای بیان یک مرز وجود دارد. منحنی مرز می تواند روی گره های شبکه واقع شود که به آن گرة مرزی می گویند. منحنی مرز می تواند مسیرهای متصل کننده گره های شبکه را قطع کند که به آن لینک مرزی می گویند. به بیان دیگر گره مرزی درون و یا خارج حوزه حل قرار دارد. شرط مرزی دیوار جامد شامل شرط عدم لغزش، لغزش آزاد یا لغزش اصطکاکی می باشد.

شرط مرزی عدم لغزش:

باتوجه به موقعیت قرارگیری دیوار(مرز با عدم لغزش) نسبت به گره های شبکه، طرح های متفاوتی در بکارگیری این شرط وجود دارد.

طرح بازگشت به عقب کامل(complete bounce back):

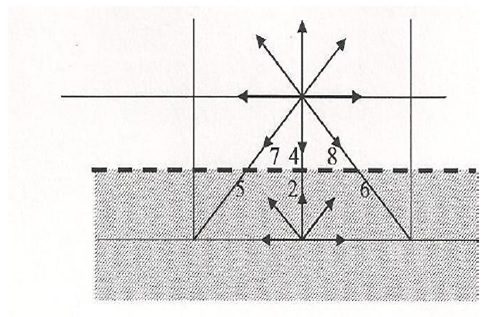
زمانی که دیوار روی گره های شبکه قرار می گیرد از این طرح استفاده می شود. تابع توزیع ذره که از گره سیال در امتداد لینک شبکه جریان می یابد، بعد از برخورد با گره دیوار در همان امتداد در جهت مخالف باز می گردد. یعنی برای گره هایی که روی مرز واقع شده اند به جای اعمال رابطه معمول برخورد، شرط بازگشت به عقب اعمال می شود که به شکل زیر نشان داده شده است. برای یافتن f_iهای مجهول در نقاط مرزی از این طرح استفاده می شود. به نحوی که f7=f5، f4=f2 و f8=f6. تمامی گره ها در مرحله برخورد شرکت می کنند.

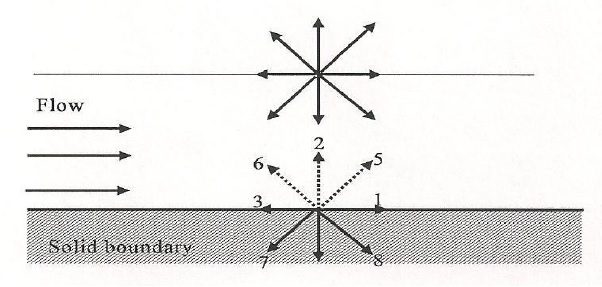
شکل طرح بازگشت به عقب کامل.

 

این انعکاس کامل صفر شدن هر دو مؤلفه عمودی و مماسی سرعت را در مرز تضمین می کند.

 

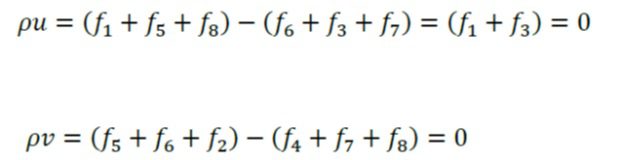
طرح بازگشت به عقب میانی(half way bounce back):

زمانی که دیوار بین گره ها قرار گیرد. این طرح با در نظر گرفتن یک دیوار موثر در موقعیت میانی بین گره سیال و مرز، دقت طرح بازگشت به عقب را بالا برده و آن را به مرتبه دوم ارتقاء می دهد. در این طرح توابع توزیع جاری شده از سیال به سمت دیوار، درون دیوار ذخیره شده و در مرحله بعد به سیال بازگردانده می شود. از لحاظ ریاضی می توان این طرح را به عنوان مثال برای مرز شمالی به صورت زیر نشان داد که (x,y) بیانگر موقعیت گره جامد درون مرز است و f4، f7 و f8 مجهول هستند.

 

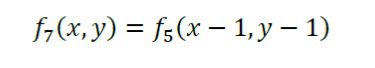
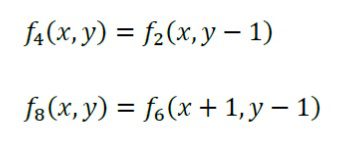
شکل طرح بازگشت به عقب با دیوار میانی.

 

شرط مرزی دیوار خمیده:

در روش های قبلی چنانچه مرز به صورت منحنی باشد، به صورت پله زیگزاگ مدل می شود. زیگزاگی بودن تابع شبکه با افزایش عدد رینولدز بدتر می شود. فیلیپوا و هانل برای اولین بار روشی برای بیان شرط مرزی خمیده مطرح کردند که برای دیوار خمیده دقت مرتبه دوم دارد. می و دیگران پایداری طرح آنها را بهبود دادند و طرح (MLS) را بیان کردند. این طرح دقت مرتبه دوم دارد و در میان طرح های مرتبه دوم از قوی ترین آنها محسوب می شود. این طرح برای تمام گره های دیوار بدون توجه به آرایش فضایی آن قابل استفاده است.

با توجه به موقعیت قرارگیری دیوار (مرز خمیده)، جهت تعیین تابع توزیع در گره w (داخل دیوار)، پارامتر جزئی     
 برای لینک موجود در گره مرزی B تعریف می شود (شکل زیر).

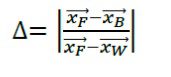
که  x که بردار موقعيت هر گره است.

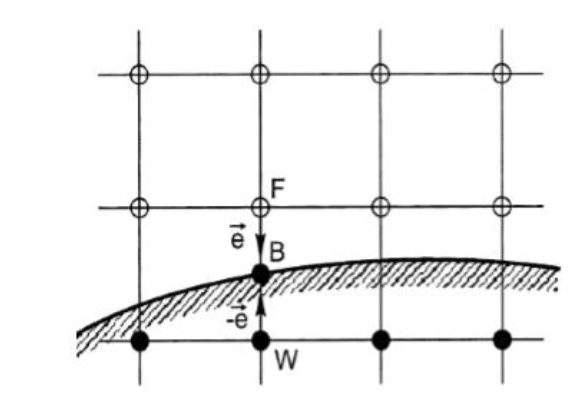
شکل مرز خمیده.

سپس تابع توزیع پس از برخورد به صورت زیر محاسبه می شود.

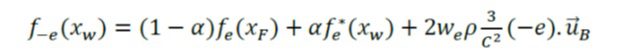
که u_B بردار سرعت دیوار در گره مرزی B، w_e ضریب وزنی که از رابطه توزیع تعادلی به دست می آید و انديس e و e- بیان کننده جهت های لینک هستند. تابع توزيع  f_e^* از رابطه زیر داده می شود.

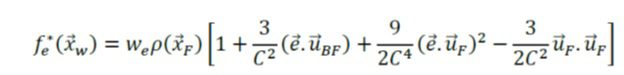
در رابطه بالا u_f  بردار سرعت سیال در گره F، a و u_BF به صورت زیر تعریف می شوند.

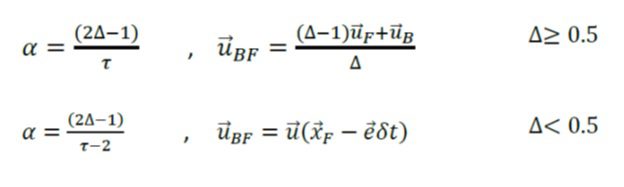
بوزیدی و همکاران یک شرط مرزی ساده تر بر اساس بازگشت به عقب برای دیوار واقع در مکان دلخواه مطرح کردند. در کار آنها هم طرح خطی و هم طرح های درجه دوم برای به دست آوردن که معادل  است، داده شده است كه تابع توزیع بعد از مرحله برخورد در گره جامد است. طرح خطی روش آنها به صورت زیر است:

 

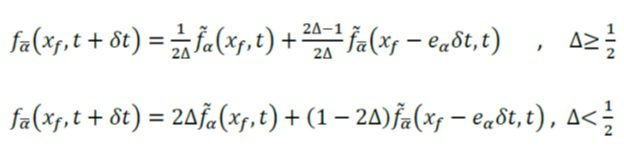
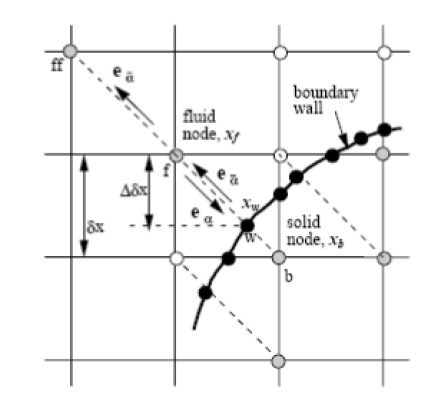
شکل نمایش پارامترهای لازم برای بیان شرط مرزی دیوار خمیده.

 

شرح پروژه:

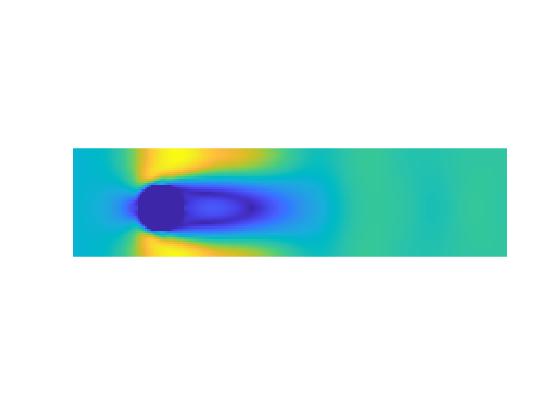
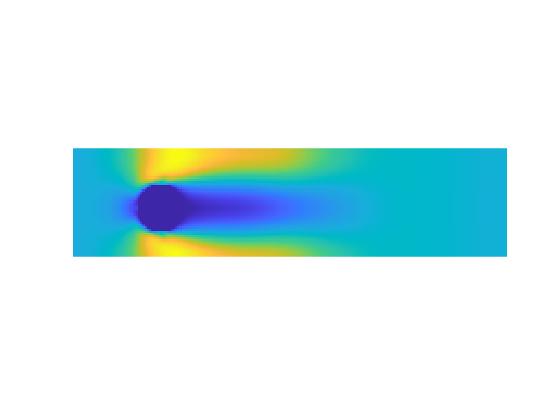
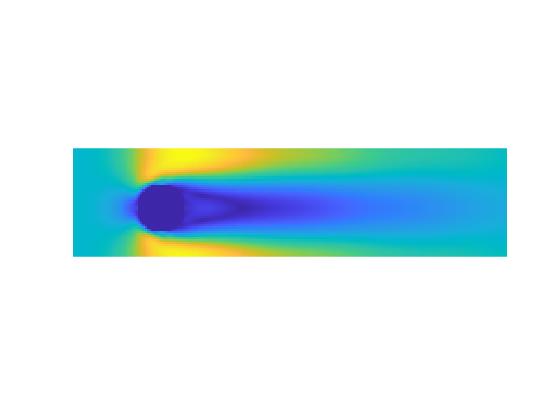
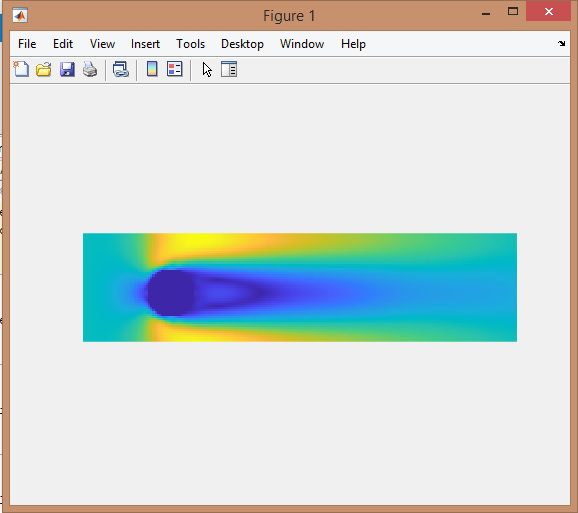
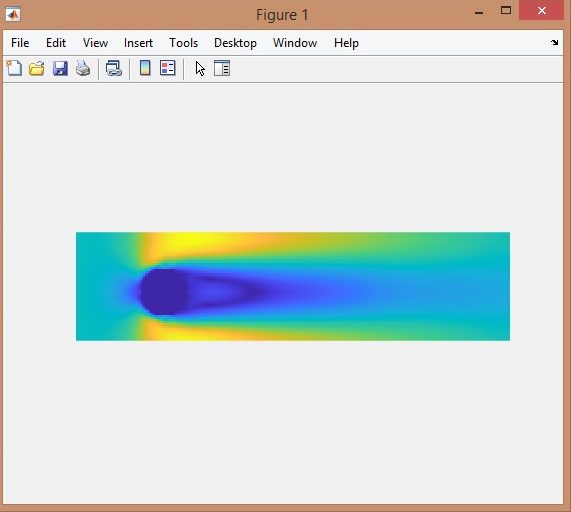
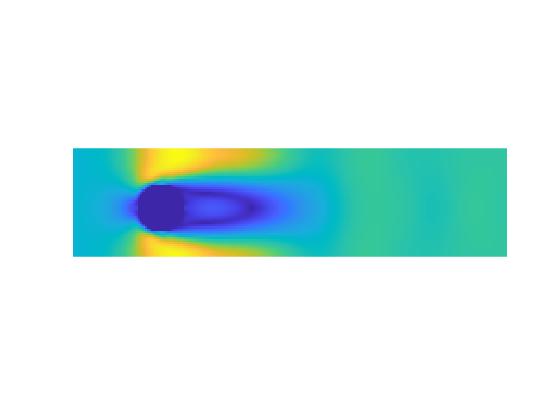
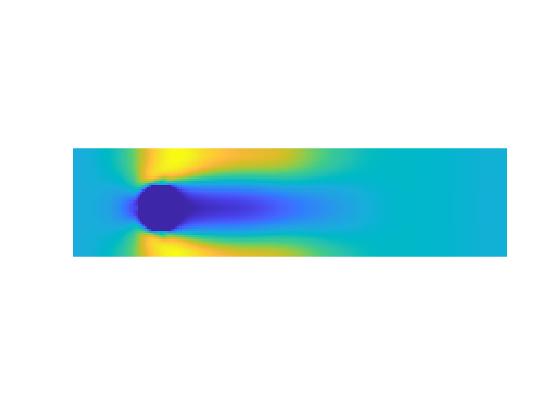
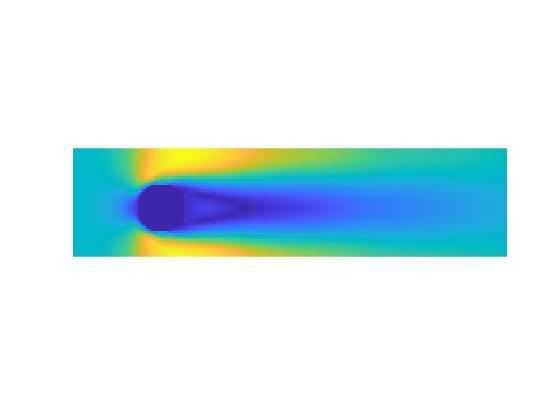
در این پروژه جریان در کانال دوبعدی با روش شبکه بولتزمن در نرم افزار متلب(MATLAB) شبیه سازی شده است. در این پروژه جریان سیال در میدان های جریان دو بعدی بر روی دیوارهای استوانه‌ ای با استفاده از شبکه بولتزمن با زمان آسودگی منفرد برای اعداد رینولدز پایین مطابق مقاله مرجع شبیه سازی شده است. این شرایط جریان برای ارزیابی دقت و پایداری تکنیک‌های مختلف در هنگام اعمال به مرزهای خمیده مورد استفاده قرار گرفته‌است. ​پنج تکنیک مختلف به کار گرفته شده‌است و نتایج آن‌ها با داده‌های موجود در مورد جریان سیال حول اجسام استوانه‌ای مقایسه شده‌است. ​

طرح بازگشت به عقب(bounce back) روشی بسیار ساده، کارآمد و آسان برای اجرای هندسه جامد در جریان است. ​با اینحال، در طرح بازگشت به عقب، دیوار در گره‌هایی از شبکه انتخاب می‌شود که در آن مکان دقیقی که شرایط مرزی برآورده می‌شوند، معمولا در یک‌گره شبکه نیست. در شبیه‌سازی جریان معلق، دیوار در میانه گره‌ها قرار داده می شود، که به عنوان طرح بازگشت به عقب در میانه شناخته می‌شود. اما همه این روش‌ها فرض می‌کنند که مرز جامد شکل پله مانند دارد که در نهایت باعث ایجاد خطا برای دیوارهای خمیده با اعداد رینولدز بالاتر می‌شود (‏شکل زیر).

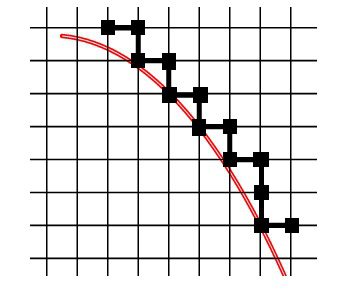
شکل گره های سیال(نقاط مربعی) نشان داده شده حول یک هندسه جامد خمیده(خط قرمز). آنچه از مرز خمیده در شبیه سازی دیده می شود، هندسه پله مانند سیاه است.

در یک طرح بازگشت به عقب ایده‌آل یا کامل(ideal bounce back)، داده‌ها باید بین گره های سیال و گره‌های جامد مانند A و B در شکل زیر، به عقب باز می گردند.

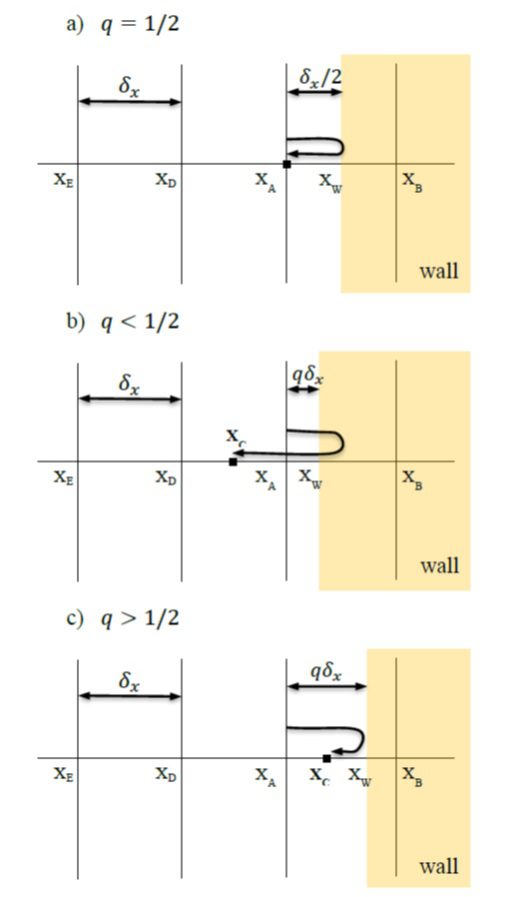
شکل طرح بازگشت به عقب کامل.

همانطور که در شکل بالا نشان‌داده شده‌است، دیوار همیشه در مرکز گره‌های جامد و سیال قرار ندارد. به عبارت دیگر، برای یک مرز خمیده، برخی گره‌ها به طور اجتناب‌ناپذیری در مکان‌های غیر از وسط قرار داده خواهند شد. ​بنابراین طرح بازگشت به عقب بایستی بهبود یابد تا قادر به کنترل مرزهای منحنی باشد. ​

روش های پیاده سازی مرزهای جامد و خمیده:

روش فیلیپوا و هانل(Filippova and Hänel):

در این معادلات u_f سرعت گره سیال واقع در نزدیک دیوار (x_f در شکل زیر) و u_w سرعت دیوار برای مورد دیوار متحرک است.

 

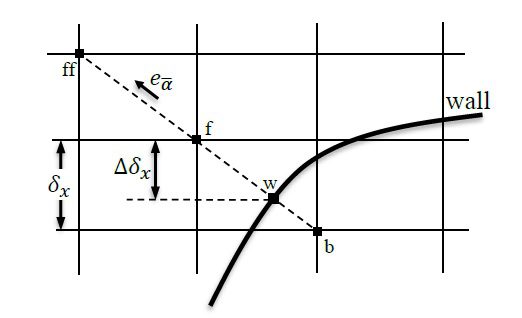
شکل مرز جامد دلخواه بین گره های شبکه.

 

روش می، لو و شای(Mei, Luo and Shyy):

این روش اصلاح شده روش فیلیپوا برای حالت  جهت بهبود ناپایداری در رابطه زیر است:

 

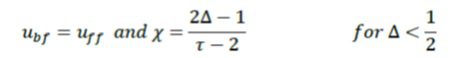
U_ff سرعت گره سیال است.

روش بوزیدی، فردوس و لالماند(Bouzidi, Firdaouss and Lallemand):

در این تکنیک، طرح های خطی و درجه دوم به صورت همزمان استفاده شده است:

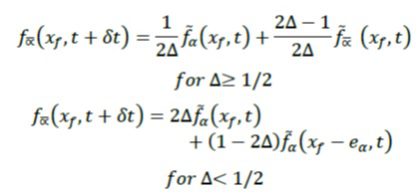
روش یو، می، و شای(Yu, Mei and Shyy):

در این روش یک رابطه برای تمامی  درنظرگرفته می شود.

 

 

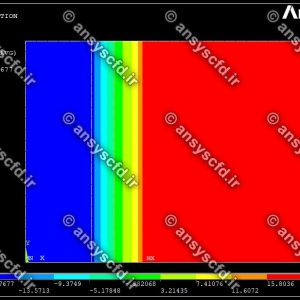
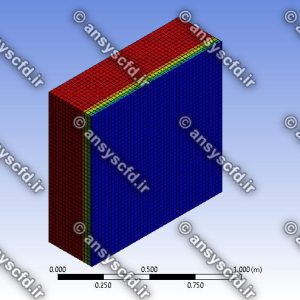
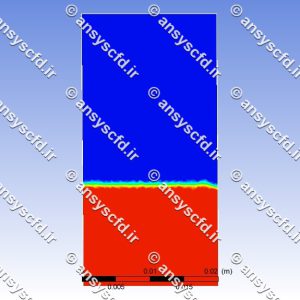
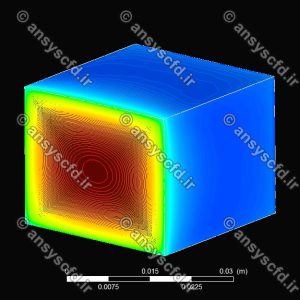
نتایج: